2023年浙教版数学八年级上册2.3 等腰三角形的性质定理 同步测试（培优）
试卷更新日期：2023-07-09 类型：同步测试
一、选择题
-
1. 如图，∠BOC＝9°，点A在OB上，且OA＝1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1 ， 得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2 ， 得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3 ， 得第3条线段A2A3…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n＝（ ）
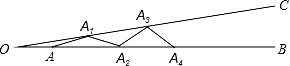A、10 B、9 C、8 D、72. 若一个等腰三角形的一条边是另一条边的k倍，我们把这样的等腰三角形叫做“k倍边等腰三角形”．如果一个等腰三角形是“4倍边等腰三角形”，且周长为18cm，则该等腰三角形底边长为（ ）A、12cm B、12cm或2cm C、2cm D、4cm或12cm3. 如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2 ， 使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3 ， 使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第2022个三角形中以A2021为顶点的底角度数是（ ）
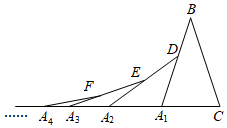A、 B、 C、 D、4. 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC交射线AC于点N，连结BN。若△BMN中有两个角相等，则∠MNB的度数不可能是（ ）
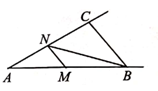A、25° B、30° C、50° D、65°5. 如图，在 中， 的平分线相交于点E， 边的垂直平分线相交于点D.若 ，则 的度数为（ ）
A、 B、 C、 D、6. 如图，在平面直角坐标系中，点A，B分别在y轴和x轴上， ，在坐标轴上找一点P，使得 是等腰三角形，则符合条件的P点的个数是（ ）
A、 B、 C、 D、7. 当题目条件出现角平分线时，我们往往可以构造等腰三角形解决问题.如图1，在 中， ，CD平分 ， ， ，求BC的长，解决办法：如图2，在BC边上取点E，使 ，连接DE，可得 且 是等腰三角形，所以BC的长为5，试通过构造等腰三角形解决问题：如图3， 中， ， ，BD平分 ，要想求AD的长，仅需知道下列哪些线段的长（ ， ， ）（ ）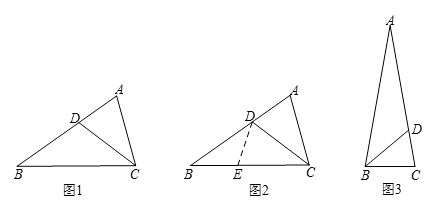
A、a和b B、b和c C、a和c D、a、b和c8. 如图，已知∠A=10°，在∠A两边上分别作点，并连接这些点，使 AB=BC=CD=DE……一直作下去，那么图中以这些线段为腰长的等腰三角形最多能找到（ ）
A、7个 B、8个 C、9个 D、10个9. 如图，在锐角△ABC中，AB＝AC＝10，S△ABC ＝25，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM＋MN的最小值是（ ）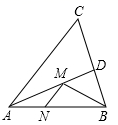
A、4 B、 C、5 D、6二、填空题
-
10. 如图，在锐角△ABC中，∠ABC＝30°，AC＝3，△ABC的面积为8，P为△ABC内部一点，分别作点P关于AB，BC，AC的对称点P1 ， P2 ， P3 ， 连接P1P2 ， PP3 ， 则2P1P2+PP3的最小值为 ．
11. 如图，在中， ， ， ， 平分 ， 是线段上的动点，是线段上的动点，则面积为 ， 的最小值为 ．
12. 如图，在中， ， ， ， 是的平分线．若P，Q分别是和上的动点，则的最小值是 ．
13. 四边形ABCD中，∠BAD＝125°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，当三角形AMN周长最小时，∠MAN的度数为.
14. 如图，在 中，AB=AC，BC=4，面积是14，AC的垂直平分线EF分别交AC，AB边于E、F点.若点D为BC边的中点，点M为线段EF上一动点，则 周长的最小值为.
15. 如图，在ABC中，∠BAC＝90°，AB＝AC，在∠BAC内部作射线AM，作点C关于AM的对称点D，连接BD并延长交AM于E，连接AD，CD.若BD＝2DE，ABD的面积为7，则四边形BACD的面积为.
三、综合题
-
16. 如图，AD为等腰△ABC的顶角∠BAC的平分线，∠ABC＝50°，在线段AD上取一点E．使得∠ACE＝20°，在线段CE上取一点F，使得∠FBC＝10°，连接BE，AF．(1)、∠EBF＝度，∠EBA＝度，∠BFE＝度；(2)、求证：BA＝BF；(3)、BE与AF的位置关系为 （直接写出）．
17. 如图，在等腰直角△ABC中，∠ACB＝90°，AC＝BC，点D是AB边上的一动点．
(1)、如图1，连接DC并延长使CE＝CD，过点E作 交AC的延长线于点F，试说明：AD＝FE；(2)、如图2，当点D运动到AB中点时，点E是DC延长线上的一点，连接AE、BE，BE与AC的延长线交于点Q．①试说明：∠CAE＝∠CBE；
②点P是AC延长线上的点，连接PE，且PE＝BE，连接BP，若AE＝8，求△BEP的面积．
18. 如图，在等腰中， ， ， 是的高，是的角平分线，与交于点当的大小变化时，的形状也随之改变.
(1)、当时，求的度数；(2)、设 ， ， 求变量与的关系式；(3)、当是等腰三角形时，求的度数.19. 在等腰△ABC中，AB＝BC，点D，E在射线BA上，BD＝DE，过点E作EF∥BC，交射线CA于点F．请解答下列问题：
(1)、当点E在线段AB上，CD是△ACB的角平分线时，如图①，求证：AE＋BC＝CF；（提示：延长CD，FE交于点M．）(2)、当点E在线段BA的延长线上，CD是△ACB的角平分线时，如图②；当点E在线段BA的延长线上，CD是△ACB的外角平分线时，如图③，请直接写出线段AE，BC，CF之间的数量关系，不需要证明；20. 在等腰△ABC中，AB=AC，点D是AC上一动点，点E在BD的延长线上，且AB=AE，AF平分∠CAE交DE于点F，连接FC．
(1)、如图1，求证：∠ABE=∠ACF；(2)、如图2，当∠ABC=60°时，在BE上取点M，使BM=EF，连接AM．求证：△AFM是等边三角形；(3)、如图3，当∠ABC=45°，且AEBC时，求证：BD=2EF．21. 已知：如图1，线段AD＝5，点B从点A出发沿射线AD方向运动，以AB为底作等腰△ABC，使得AC＝BC＝AB．
(1)、如图2，当AB＝10时，求证：CD⊥AB；(2)、当△BCD是以BC为腰的等腰三角形时，求BC的长；(3)、当AB＞5时，在线段BC上是否存在点E，使得△BDE与△ACD全等，若存在，求出BC的长；若不存在，请说明理由；(4)、作点A关于直线 CD的对称点A′，连结 CA′当CA′∥AB时，求CA′＝（请直接写出答案）．22. 如图，已知△ABC是等腰三角形，CA＝CB，∠ACB是锐角，∠ACB＝α．点M在边AC上，点N在边BC上（点M、点N不与所在线段端点重合），BN＝AM，连接AN，BM，射线AG∥BC，延长BM交射线AG于点D，点E在NA的延长线上，且AE＝DE．
(1)、△BCM与△ACN全等吗？请说明理由；(2)、请求出∠BDE的度数．（用含α的代数式表示）23. 定义：顶角相等且顶点重合的两个等腰三角形叫做对顶三角形．如图1，在 OAB与 OCD中，OA=OB ， OC=OD ， ∠AOB=∠COD ．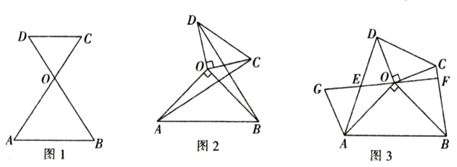
(1)、如图1， OAB与 OCD是对顶三角形，且A ， O ， C三点共线请判断AB与CD的位置关系，并说明理由．(2)、如图2， OAB与 OCD是对顶三角形，∠AOB=∠COD=90°，连接AC ， BD ， 试探究线段AC ， BD之间的关系，并说明理由．(3)、如图3， OAB与 OCD是对顶三角形，∠AOB=∠COD=90°，连接AD ， BC ， 取AD的中点E ， 连接EO并延长交BC于点F ， 延长OE至点G ， 使EG=OE ， 连接AG ， 求证：EF⊥BC ．