浙江省2023年中考数学真题分类汇编11 解直角三角形

试卷更新日期：2023-07-09 类型：二轮复习

进入出卷网下载

一、选择题

1. 如图，矩形 $A B C D$ 的对角线 $A C ， B D$ 相交于点 $O$ ．若 $∠ A O B = 60 °$ ，则 $\frac{A B}{B C} =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3} - 1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
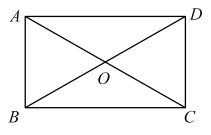2. 如图，在菱形ABCD中，AB=1，∠DAB=60°，则AC的长为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

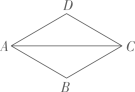查看试题解析
3. 如图，在四边形ABCD中，AD∥BC，∠C=45°，以AB为腰作等腰直角三角形BAE，顶点E恰好落在CD边上，若AD=1．则CE的长是（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、2 D、1

查看试题解析
4. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（ $△ D A E ， △ A B F ， △ B C G ， △ C D H$ ）和中间一个小正方形 $E F G H$ 拼成的大正方形 $A B C D$ 中， $∠ A B F > ∠ B A F$ ，连接 $B E$ ．设 $∠ B A F = α ， ∠ B E F = β$ ，若正方形 $E F G H$ 与正方形 $A B C D$ 的面积之比为 $1 ： n ， t a n α = t a n^{2} β$ ，则 $n =$ （）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

5. 如图，分别以a，b，m，n为边长作正方形，已知m>n且满足am-bn=2．an+bm=4．

(1)、若a=3，b=4，则图1阴影部分的面积是；

(2)、若图1阴影部分的面积为3．图2四边形ABCD的面积为5，则图2阴影部分的面积是。

查看试题解析

三、计算题

6. 计算： $(- 2023)^{0} + \sqrt{4} - 2 s i n 30 ° + | - 5 |$ .

查看试题解析

四、解答题

7. 如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A-D-C．已知DC⊥BC，AB⊥BC．∠A=60°，AB=11m，CD=4m．求管道A-D-C的总长.

查看试题解析
8. 教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC， $∠ B A C = 90 °$ ．黑板上投影图像的高度 $A B = 120 c m$ ， CB与AB的夹角 $∠ B = 33.7 °$ ，求AC的长．（结果精确到1cm．参考数据： $s i n 33.7 ° \approx 0.55$ ， $c o s 33.7 ° \approx 0.83$ ， $t a n 33.7 ° \approx 0.67$ ）

查看试题解析
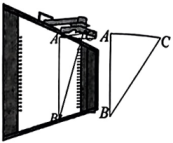9. 如图1，AB为半圆 $O$ 的直径， $C$ 为BA延长线上一点，CD切半圆于点 $D ， B E ⊥ C D$ ，交CD延长线于点 $E$ ，交半圆于点 $F$ ，已知 $O A = \frac{3}{2} ， A C = 1$ .如图2，连结AF，P为线段AF上一点，过点 $P$ 作BC的平行线分别交CE，BE于点M，N，过点 $P$ 作 $P H ⊥ A B$ 于点 $H$ .设 $P H = x ， M N = y$ .

(1)、求CE的长和 $y$ 关于 $x$ 的函数表达式.

(2)、当 $P H < P N$ ，且长度分别等于 $P H ， P N$ ， $a$ 的三条线段组成的三角形与 $△ B C E$ 相似时，求 $a$ 的值.

(3)、延长 $P N$ 交半圆 $O$ 于点 $Q$ ，当 $N Q = \frac{15}{4} x - 3$ 时，求 $M N$ 的长.

查看试题解析
10. 图1是某款篮球架，图2是其示意图，立柱 $O A$ 垂直地面 $O B$ ，支架 $C D$ 与 $O A$ 交于点 $A$ ，支架 $C G ⊥ C D$ 交 $O A$ 于点 $G$ ，支架 $D E$ 平行地面 $O B$ ，篮筐 $E F$ 与支架 $D E$ 在同一直线上， $O A = 2.5$ 米， $A D = 0.8$ 米， $∠ A G C = 3 2^{°}$ .

(1)、求 $∠ G A C$ 的度数.

(2)、某运动员准备给篮筐挂上篮网，如果他站在凳子上，最高可以把篮网挂到离地面3米处，那么他能挂上篮网吗？请通过计算说明理由.
（参考数据： $s i n 3 2^{°} \approx 0.53 ， c o s 3 2^{°} \approx 0.85 ， t a n 3 2^{°} \approx 0.62$ ）

查看试题解析
11. 某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图1所示．

(1)、如图2，在 $P$ 点观察所测物体最高点 $C$ ，当量角器零刻度线上 $A ， B$ 两点均在视线 $P C$ 上时，测得视线与铅垂线所夹的锐角为 $α$ ，设仰角为 $β$ ，请直接用含 $α$ 的代数式示 $β$ ．

(2)、如图3，为了测量广场上空气球 $A$ 离地面的高度，该小组利用自制简易测角仪在点 $B ， C$ 分别测得气球 $A$ 的仰角 $∠ A B D$ 为 $37 °$ ， $∠ A C D$ 为 $45 °$ ，地面上点 $B ， C ， D$ 在同一水平直线上， $B C = 20 m$ ，求气球 $A$ 离地面的高度 $A D$ ．（参考数据： $s i n 37 ° \approx 0.60 ， c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ）

查看试题解析
12. 图1是某住宅单元楼的人脸识别系统（整个头部需在摄像头视角围内才能被识别），其示意图如图2，摄像头A的仰角、俯角均为15°，摄像头高度 $O A = 160 c m$ ，识别的最远水平距离 $O B = 150 c m$ 。

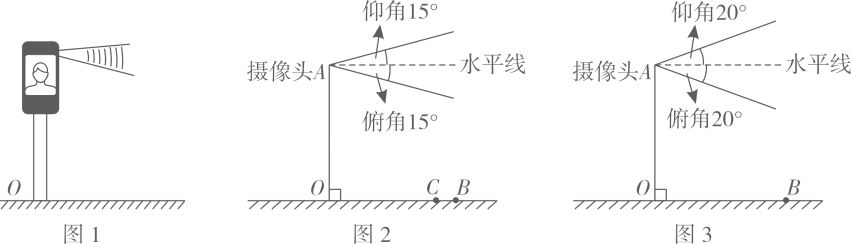(1)、身高 $208 c m$ 的小杜，头部高度为 $26 c m$ ，他站在离摄像头水平距离 $130 c m$ 的点C处，请问小杜最少需要下蹲多少厘米才能被识别。

(2)、身高 $120 c m$ 的小若，头部高度为 $15 c m$ ，踮起脚尖可以增高 $3 c m$ ，但仍无法被识别．社区及时将摄像头的仰角、俯角都调整为 $20 °$ （如图3），此时小若能被识别吗？请计算说明。
（精确到 $0 ． 1 c m$ ，参考数据 $s i n 15 ° \approx 0 ， 26 ， c o s 15 ° \approx 0.97 ， t a n 15 ° \approx 0.27 ， s i n 20 ° \approx 0.34 ， c o s 20 ° \approx 0.94 ， t a n 20 ° \approx 0.36$ ）

查看试题解析
13. 如图，在⊙O中，AB是一条不过圆心O的弦，点C，D是 $\overset{⌢}{A B}$ 的三等分点，直径CE交AB于点F，连结AD交CF于点G，连结AC，过点C的切线交BA的延长线于点H．

(1)、求证：AD∥HC；

(2)、若 $\frac{O G}{G C}$ =2，求tan∠FAG的值；

(3)、连结BC交AD于点N．若⊙O的半径为5．
下面三个问题，依次按照易、中、难排列，对应的分值为2分、3分、4分，请根据自己的认知水平，选择其中一道问题进行解答。

①若OF= $\frac{5}{2}$ ，求BC的长；

②若AH= $\sqrt{10}$ ，求△ANB的局长：

③若HF·AB=88．求△BHC的面积.

查看试题解析

14. 根据背景素材，探索解决问题.

测算发射塔的高度
背景素材	某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN（如图1）.他们通过自制的测倾仪（如图2）在A，B，C三个位置观测，测倾仪上的示数如图3所示.

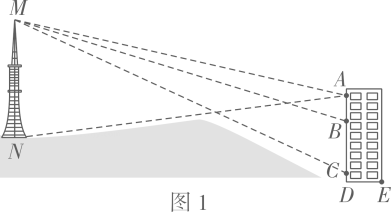
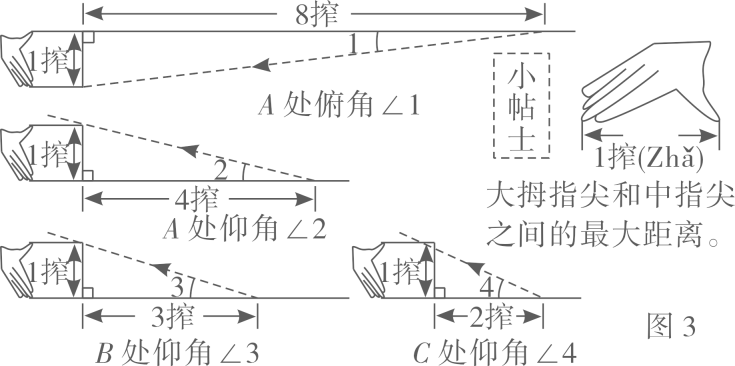
	经讨论，只需选择其中两个合适的位置，通过测量﹑换算就能计算发射塔的高度.
问题解决
任务1	分析规划	选择两个观测位置：点 ▲ 和点 ▲ 。
	获取数据	写出所选位置观测角的正切值，并量出观测点之间的图上距离.
任务2	推理计算	计算发射塔的图上高度MN.
任务3	换算高度	楼房实际宽度DE为12米，请通过测量换算发射塔的实际高度.

注：测量时，以答题纸上的图上距离为准，并精确到1mm.

查看试题解析

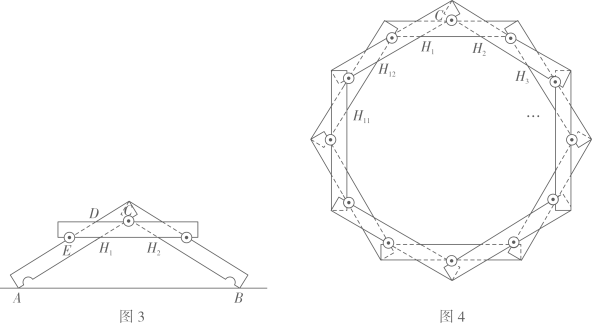
15. 问题：如何设计“倍力桥”的结构？

图1是搭成的“倍力桥”，纵梁a，c夹住横梁 $b$ ，使得横梁不能移动，结构稳固.

图2是长为 $l (c m)$ ，宽为 $3 c m$ 的横梁侧面示意图，三个凹槽都是半径为 $1 c m$ 的半圆.圆心分别为 $O_{1} ， O_{2} ， O_{3} ， O_{1} M = O_{1} N ， O_{2} Q = O_{3} P$ $= 2 c m$ ，纵梁是底面半径为 $1 c m$ 的圆柱体.用相同规格的横梁、纵梁搭“桥”，间隙忽略不计.

探究1：图3是“桥”侧面示意图，A，B为横梁与地面的交点，C，E为圆心，D，H₁ ， H₂是横梁侧面两边的交点.测得AB=32cm，点C到AB的距离为12cm.试判断四边形CDEH₁的形状，并求 $l$ 的值.

探究2：若搭成的“桥”刚好能绕成环，其侧面示意图的内部形成一个多边形.

①若有12根横梁绕成环，图4是其侧面示意图，内部形成十二边形 $H_{1} H_{2} H_{3} … H_{12}$ ，求 $l$ 的值；

②若有n根横梁绕成的环（n为偶数，且n≥6），试用关于n的代数式表示内部形成的多边形 $H_{1} H_{2} H_{3} … H_{n}$ 的周长.

查看试题解析