浙江省2023年中考数学真题分类汇编10 图形的相似
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )
 A、 B、 C、 D、2. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( )
A、 B、 C、 D、2. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( ) A、12 B、14 C、18 D、243. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( )
A、12 B、14 C、18 D、243. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( ) A、 B、 C、2 D、14. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( )
A、 B、 C、2 D、14. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( ) A、的面积 B、的面积 C、的面积 D、的面积5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、的面积 B、的面积 C、的面积 D、的面积5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )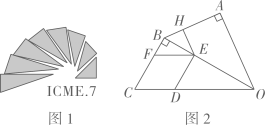 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 小慧同学在学习了九年级上册“4.1比例线段”3节课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值+感受这种特殊化的学习过程.
 7. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
7. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示). 8. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .
8. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .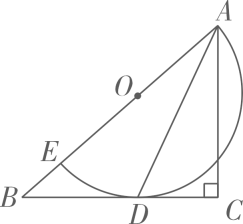
三、解答题
-
9. 如图,在中,直径垂直弦于点 , 连接 , 作于点 , 交线段于点(不与点重合),连接 .
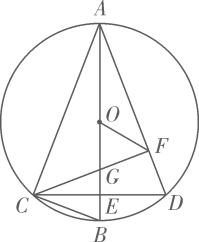 (1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.10. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 .
(1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.10. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 . (1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.11. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.
(1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.11. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.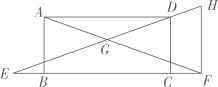 (1)、求证:.(2)、当时,求EF的长.12. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设.
(1)、求证:.(2)、当时,求EF的长.12. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设. (1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.13. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且.
(1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.13. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且. (1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.
(1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.①如图2,当点落在射线上时,求的长.
②当当是直角三角形时,求的长.
14. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D. (1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.15. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .
(1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.15. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .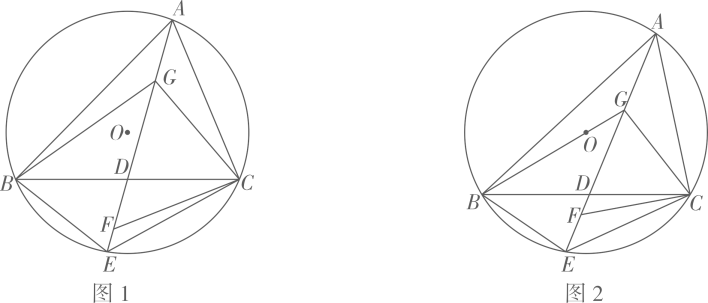 (1)、求的度数.(2)、①求证: .
(1)、求的度数.(2)、①求证: .②若 , 求的值,
(3)、如图2,当点O恰好在上且时,求的长.16. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .17. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H.
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .17. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H. (1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.
(1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.下面三个问题,依次按照易、中、难排列,对应的分值为2分、3分、4分,请根据自己的认知水平,选择其中一道问题进行解答。
①若OF= , 求BC的长;
②若AH= , 求△ANB的局长:
③若HF·AB=88.求△BHC的面积.