浙江省2023年中考数学真题分类汇编08 圆
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
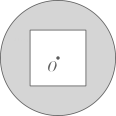 A、 B、2 C、 D、2. 如图,在中,半径互相垂直,点在劣弧上.若 , 则( )
A、 B、2 C、 D、2. 如图,在中,半径互相垂直,点在劣弧上.若 , 则( ) A、 B、 C、 D、3. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( )
A、 B、 C、 D、3. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
4. 若扇形的圆心角为 , 半径为18,则它的弧长为。5. 如图,圆锥形烟囱帽的底面半径为 , 母线长为 , 则烟囱帽的侧面积为 . (结果保留)
 6. 如图,四边形内接于圆 , 若 , 则的度数是.
6. 如图,四边形内接于圆 , 若 , 则的度数是. 7. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 .
7. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 . 8. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .
8. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .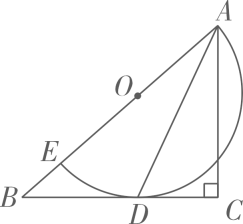 9. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。
9. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。 10. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm.
10. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm. 11. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。
11. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。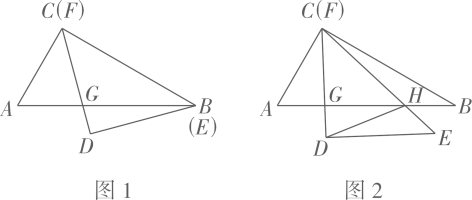 12. 图1是方格绘成的七巧板图案,每个小方格的边长为 , 现将它前拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为.若点A,N,M在同一直线上, , 则题字区域的面积为.
12. 图1是方格绘成的七巧板图案,每个小方格的边长为 , 现将它前拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为.若点A,N,M在同一直线上, , 则题字区域的面积为.
三、解答题
-
13. 如图,在中,直径垂直弦于点 , 连接 , 作于点 , 交线段于点(不与点重合),连接 .
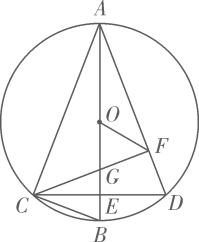 (1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.14. 如图,是的直径,是上一点,过点作的切线 , 交的延长线于点 , 过点作于点.
(1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.14. 如图,是的直径,是上一点,过点作的切线 , 交的延长线于点 , 过点作于点. (1)、若 , 求的度数.(2)、若 , 求的长.15. 如图,点在第一象限内,与轴相切于点 , 与轴相交于点C,D.连结AB,过点作于点.
(1)、若 , 求的度数.(2)、若 , 求的长.15. 如图,点在第一象限内,与轴相切于点 , 与轴相交于点C,D.连结AB,过点作于点. (1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.16. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设.
(1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.16. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设. (1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.17. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
(1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.17. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D. (1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.18. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .
(1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.18. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .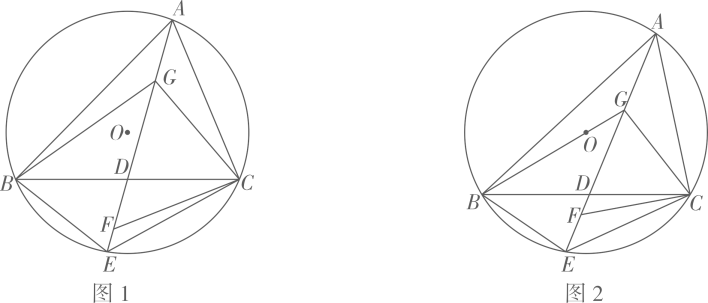 (1)、求的度数.(2)、①求证: .
(1)、求的度数.(2)、①求证: .②若 , 求的值,
(3)、如图2,当点O恰好在上且时,求的长.19. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .20. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H.
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .20. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H. (1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.
(1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.下面三个问题,依次按照易、中、难排列,对应的分值为2分、3分、4分,请根据自己的认知水平,选择其中一道问题进行解答。
①若OF= , 求BC的长;
②若AH= , 求△ANB的局长:
③若HF·AB=88.求△BHC的面积.