浙江省2023年中考数学真题分类汇编07 四边形
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 如图,矩形的对角线相交于点 . 若 , 则( )
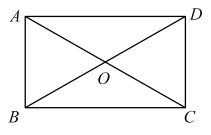 A、 B、 C、 D、2. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( )
A、 B、 C、 D、2. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( ) A、5 B、4 C、3 D、23. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、5 B、4 C、3 D、23. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )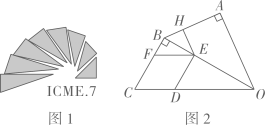 A、 B、 C、 D、4. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
A、 B、 C、 D、4. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).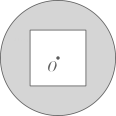 A、 B、2 C、 D、5. 如图,以钝角三角形ABC最长边BC为边向外作矩形 , 连结 , 设 , , 的面积分别为 , 若要求出的值,只需知道( )
A、 B、2 C、 D、5. 如图,以钝角三角形ABC最长边BC为边向外作矩形 , 连结 , 设 , , 的面积分别为 , 若要求出的值,只需知道( ) A、的面积 B、的面积 C、的面积 D、矩形的面积6. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:
A、的面积 B、的面积 C、的面积 D、矩形的面积6. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为( ) A、 B、 C、 D、7. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
A、 B、 C、 D、7. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )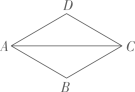 A、 B、1 C、 D、8. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( )
A、 B、1 C、 D、8. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( ) A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形
A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形二、填空题
-
9. 如图,把两根钢条OA,OB的一个端点连在一起,点C,D分别是OA,OB的中点.若CD=4cm,则该工件内槽宽AB的长为cm.
 10. 如图,在菱形中, , 连结 , 以点为圆心,长为半径作弧,交直线于点 , 连结 , 则的度数是.
10. 如图,在菱形中, , 连结 , 以点为圆心,长为半径作弧,交直线于点 , 连结 , 则的度数是.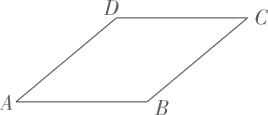 11. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是.
11. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是. 12. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .
12. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .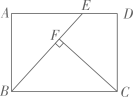 13. 如图,分别以a,b,m,n为边长作正方形,已知m>n且满足am-bn=2.an+bm=4.
13. 如图,分别以a,b,m,n为边长作正方形,已知m>n且满足am-bn=2.an+bm=4. (1)、若a=3,b=4,则图1阴影部分的面积是;(2)、若图1阴影部分的面积为3.图2四边形ABCD的面积为5,则图2阴影部分的面积是 。14. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
(1)、若a=3,b=4,则图1阴影部分的面积是;(2)、若图1阴影部分的面积为3.图2四边形ABCD的面积为5,则图2阴影部分的面积是 。14. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
三、解答题
-
15. 如图,平行四边形的对角线相交于点 , 点在对角线上,且 , 连接 , .
 (1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.16. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 .
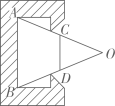
(1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.16. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 . (1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.17. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.
(1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.17. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.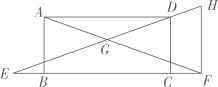 (1)、求证:.(2)、当时,求EF的长.18. 如图,在正方形中,是对角线上的一点(与点不重合),分别为垂足.连结 , 并延长交于点.
(1)、求证:.(2)、当时,求EF的长.18. 如图,在正方形中,是对角线上的一点(与点不重合),分别为垂足.连结 , 并延长交于点. (1)、求证:.(2)、判断与是否垂直,并说明理由.19. 如图,四边形ABCD中, , , BD为对角线.
(1)、求证:.(2)、判断与是否垂直,并说明理由.19. 如图,四边形ABCD中, , , BD为对角线. (1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).20. 定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角.
(1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).20. 定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角. (1)、如图1,在四边形中, , 对角线平分 . 求证:四边形为邻等四边形.(2)、如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.(3)、如图3,四边形是邻等四边形, , 为邻等角,连接 , 过B作交的延长线于点E.若 , 求四边形的周长.21. 如图,在菱形ABCD中,于点E,于点F,连结EF。
(1)、如图1,在四边形中, , 对角线平分 . 求证:四边形为邻等四边形.(2)、如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.(3)、如图3,四边形是邻等四边形, , 为邻等角,连接 , 过B作交的延长线于点E.若 , 求四边形的周长.21. 如图,在菱形ABCD中,于点E,于点F,连结EF。 (1)、求证:;(2)、若 , 求的度数。22. 如图,点在第一象限内,与轴相切于点 , 与轴相交于点C,D.连结AB,过点作于点.
(1)、求证:;(2)、若 , 求的度数。22. 如图,点在第一象限内,与轴相切于点 , 与轴相交于点C,D.连结AB,过点作于点. (1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.23. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且.
(1)、求证:四边形为矩形.(2)、已知的半径为 , 求弦的长.23. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且. (1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.
(1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.①如图2,当点落在射线上时,求的长.
②当当是直角三角形时,求的长.
24. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .25. 问题:如何设计“倍力桥”的结构?
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .25. 问题:如何设计“倍力桥”的结构?图1是搭成的“倍力桥”,纵梁a,c夹住横梁 , 使得横梁不能移动,结构稳固.
图2是长为 , 宽为的横梁侧面示意图,三个凹槽都是半径为的半圆.圆心分别为 , 纵梁是底面半径为的圆柱体.用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.


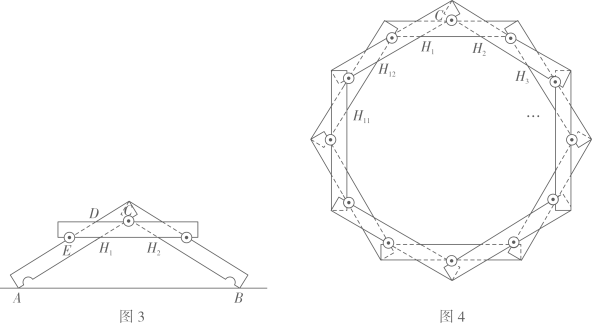
探究1:图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,D,H1 , H2是横梁侧面两边的交点.测得AB=32cm,点C到AB的距离为12cm.试判断四边形CDEH1的形状,并求的值.
探究2:若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.
①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求的值;
②若有n根横梁绕成的环(n为偶数,且n≥6),试用关于n的代数式表示内部形成的多边形的周长.