浙江省2023年中考数学真题分类汇编06 平行线与三角形
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )A、 B、 C、 D、2. 如图,已知 , 则的度数是( )
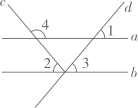 A、 B、 C、 D、3. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
A、 B、 C、 D、3. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ). A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( ) A、 B、 C、 D、5. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( )
A、 B、 C、 D、5. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( ) A、12 B、14 C、18 D、246. 如图,在Rt中, , 以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点.若 , 则的值是( )
A、12 B、14 C、18 D、246. 如图,在Rt中, , 以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点.若 , 则的值是( )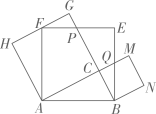 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
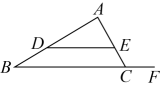 8. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 .
8. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 . 9. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。
9. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。 10. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.
10. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.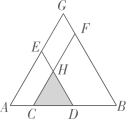 (1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .11. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 .
(1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .11. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 . 12. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。
12. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。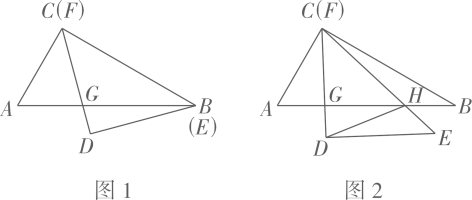
三、作图题
-
13. 如图,在的方格纸ABCD中,每个小方格的边长为1.已知格点 , 请按要求画格点三角形(顶点均在格点上).
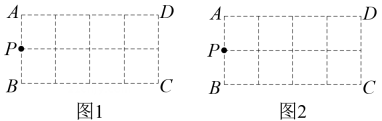 (1)、在图1中画一个等腰三角形PEF,使底边长为 , 点在BC上,点在AD上,再画出该三角形绕矩形ABCD的中心旋转后的图形.(2)、在图2中画一个Rt , 使 , 点在上,点在AD上,再画出该三角形向右平移1个単位后的图形.14. 如图,为制作角度尺,将长为10,宽为4的矩形OABC分割成4×10的小正方形网格.在该矩形边上取点P,来表示∠POA的度数.阅读以下作图过程,并回答下列问题:
(1)、在图1中画一个等腰三角形PEF,使底边长为 , 点在BC上,点在AD上,再画出该三角形绕矩形ABCD的中心旋转后的图形.(2)、在图2中画一个Rt , 使 , 点在上,点在AD上,再画出该三角形向右平移1个単位后的图形.14. 如图,为制作角度尺,将长为10,宽为4的矩形OABC分割成4×10的小正方形网格.在该矩形边上取点P,来表示∠POA的度数.阅读以下作图过程,并回答下列问题:作法(如图)
结论
①在上取点 , 使.
,
点表示.
②以为圆心,8为半径作弧,与交于点
,
点表示.
③分别以 , 为圆心,大于长度一半的长为半径作弧,相交于点E,F,连结EF与BC相交于点.
…
④以为圆心,的长为半径作弧,与射线交于点 , 连结交于点.
…
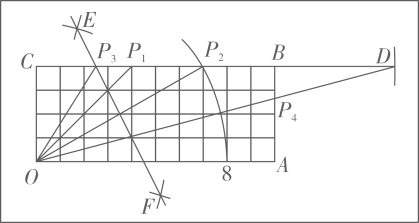 (1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).
(1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).四、综合题
-
15. 某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作.并进行猜想和证明。
 (1)、用三角板分别取AB,AC的中点D,E,连结DE,画AF⊥DE于点F;(2)、用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无继隙无重叠).并用三角板画出示意图:(3)、请判断(2)中所拼的四边形的形状,并说明理由
(1)、用三角板分别取AB,AC的中点D,E,连结DE,画AF⊥DE于点F;(2)、用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无继隙无重叠).并用三角板画出示意图:(3)、请判断(2)中所拼的四边形的形状,并说明理由