浙江省2023年中考数学真题分类汇编05 二次函数
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
 B、
B、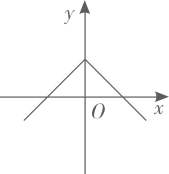 C、
C、 D、
D、 2. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限3. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为4. 已知二次函数 , 下列说法正确的是( )A、点在该函数的图象上 B、当且时, C、该函数的图象与x轴一定有交点 D、当时,该函数图象的对称轴一定在直线的左侧5. 一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2 , 那么球弹起后又回到地面所花的时间t(秒)是( )A、5 B、10 C、1 D、2
2. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限3. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为4. 已知二次函数 , 下列说法正确的是( )A、点在该函数的图象上 B、当且时, C、该函数的图象与x轴一定有交点 D、当时,该函数图象的对称轴一定在直线的左侧5. 一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2 , 那么球弹起后又回到地面所花的时间t(秒)是( )A、5 B、10 C、1 D、2二、填空题
-
6. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.

三、解答题
-
7. 设二次函数 , ( , 是实数).已知函数值和自变量的部分对应取值如下表所示:
…
0
1
2
3
…
…
1
1
…
(1)、若 , 求二次函数的表达式;(2)、写出一个符合条件的的取值范围,使得随的增大而减小.(3)、若在m、n、p这三个实数中,只有一个是正数,求的取值范围.8. 如图,已知二次函数图象经过点和 . (1)、求该二次函数的表达式及图象的顶点坐标.(2)、当时,请根据图象直接写出x的取值范围.9. 已知二次函数.(1)、当时,
(1)、求该二次函数的表达式及图象的顶点坐标.(2)、当时,请根据图象直接写出x的取值范围.9. 已知二次函数.(1)、当时,①求该函数图象的顶点坐标.
②当时,求的取值范围.
(2)、当时,的最大值为2;当时,的最大值为3,求二次函数的表达式.10. 在二次函数中,(1)、若它的图象过点 , 则t的值为多少?(2)、当时,y的最小值为 , 求出t的值:(3)、如果都在这个二次函数的图象上,且 , 求m的取值范围。11. 已知点(-m,0)和(3m,0)在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图象上。(1)、当m=-1时,求a和b的值:(2)、若二次函数的图象经过点A(n,3)且点A不在坐标轴上,当-2<m<-1时,求n的取值范围:(3)、求证:b2+4a=0.12. 一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以为原点建立如图所示直角坐标系.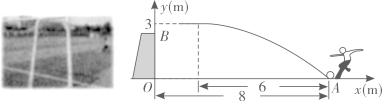 (1)、求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。(2)、对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处?13. 【问题背景】
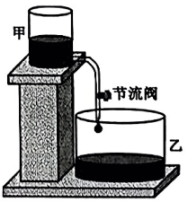
(1)、求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。(2)、对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处?13. 【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】
综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如下表:
流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务1 分别计算表中每隔10min水面高度观察值的变化量.
【建立模型】
小组讨论发现:“ , ”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2 利用时,;时,这两组数据求水面高度h与流水时间t的函数解析式.
【反思优化】
经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差.小组决定优化函数解析式,减少偏差.通过查阅资料后知道:t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和 , 记为w;w越小,偏差越小.
任务3 ⑴计算任务2得到的函数解析式的w值.
⑵请确定经过的一次函数解析式,使得w的值最小.
【设计刻度】
得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4 请你简要写出时间刻度的设计方案.
14. 如图,直线与轴,轴分别交于点A,B,抛物线的顶点在直线AB上,与轴的交点为C,D,其中点的坐标为.直线BC与直线PD相交于点. (1)、如图2,若抛物线经过原点.
(1)、如图2,若抛物线经过原点.①求该抛物线的函数表达式;②求的值.
(2)、连结与能否相等?若能,求符合条件的点的横坐标;若不能,试说明理由.
-