浙江省2023年中考数学真题分类汇编04 一次函数与反比例函数
试卷更新日期:2023-07-09 类型:二轮复习
一、选择题
-
1. 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位留的坐标为 , 则“炮”所在位置的坐标为( ).
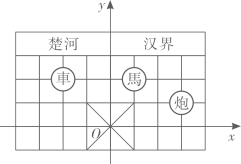 A、 B、 C、 D、2. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、53. 在平面直角坐标系中,将点先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )A、 B、 C、 D、4. 在平面直角坐标系中,点P(-1,m2+1)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A、 B、 C、 D、2. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、53. 在平面直角坐标系中,将点先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )A、 B、 C、 D、4. 在平面直角坐标系中,点P(-1,m2+1)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )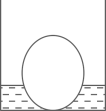 A、
A、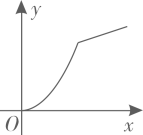 B、
B、 C、
C、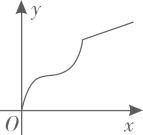 D、
D、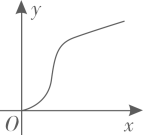 6. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限7. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
6. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限7. 已知点在同一个函数图象上,则这个函数图象可能是( )A、 B、
B、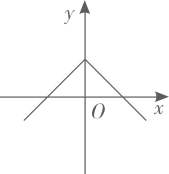 C、
C、 D、
D、 8. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、9. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( )
8. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、9. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( ) A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称10. 如果100N的压力F作用于物体上,产生的压强p要大于1000Pa,则下列关于物体受力面积S(m2)的说法正确的是( )A、S小于0.1m2 B、S大于0.1m2 C、S小于10m2 D、S大于10m211. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( )
A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称10. 如果100N的压力F作用于物体上,产生的压强p要大于1000Pa,则下列关于物体受力面积S(m2)的说法正确的是( )A、S小于0.1m2 B、S大于0.1m2 C、S小于10m2 D、S大于10m211. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( ) A、或 B、或 C、或 D、或12. 如图,一次函数的图像与反比例函数的图像相交于两点,点的横坐标为1,点的横坐标为 , 当时,的取值范围是( )
A、或 B、或 C、或 D、或12. 如图,一次函数的图像与反比例函数的图像相交于两点,点的横坐标为1,点的横坐标为 , 当时,的取值范围是( ) A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或二、填空题
-
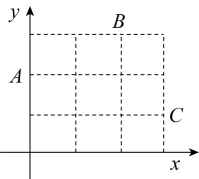
13. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .
 14. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对气缸壁所产生的压强与气缸内气体的体积成反比例,关于的函数图象如图所示.若压强由加压到 , 则气体体积压缩了.
14. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对气缸壁所产生的压强与气缸内气体的体积成反比例,关于的函数图象如图所示.若压强由加压到 , 则气体体积压缩了.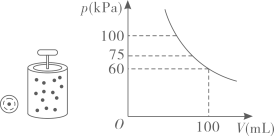 15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是.
15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是. 16. 如图,点A,B分别在函数图象的两支上(A在第一象限),连接AB交x轴于点C.点D,E在函数图象上,轴,轴,连接 . 若 , 的面积为9,四边形的面积为14,则的值为 , a的值为 .
16. 如图,点A,B分别在函数图象的两支上(A在第一象限),连接AB交x轴于点C.点D,E在函数图象上,轴,轴,连接 . 若 , 的面积为9,四边形的面积为14,则的值为 , a的值为 .
三、解答题
-
17. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
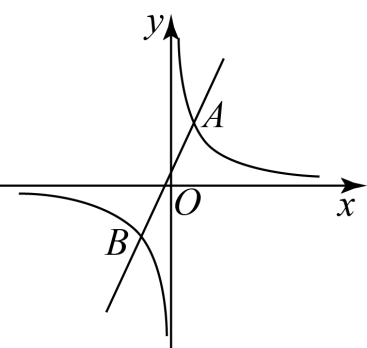 (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.18. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点.
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.18. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点. (1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.19. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象.
(1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.19. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象. (1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.20. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, .
(1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.20. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, .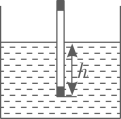 (1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .21. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地
(1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .21. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地 地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.  (1)、求大巴离营地的路程s与所用时间t的函数表达式及a的值,(2)、求部队官兵在仓库领取物资所用的时间.22. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
(1)、求大巴离营地的路程s与所用时间t的函数表达式及a的值,(2)、求部队官兵在仓库领取物资所用的时间.22. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
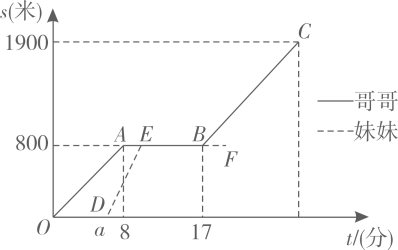 (1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
(1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值;
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.23. 我市“共富工坊"问梅借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同,看图解答下列问题: (1)、直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)、求方案二y关于x的函数表达式;(3)、如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
(1)、直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)、求方案二y关于x的函数表达式;(3)、如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.