（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（培优卷）

试卷更新日期：2023-07-08 类型：同步测试

进入出卷网下载

一、选择题

1. 有理数 $a ， b ， c$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）
① $a b c > 0$ ；② $a + c < b$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ ；④ $| a - b | - | b - c | = | a - c |$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 四个各不相等的整数 $a 、 b 、 c 、 d$ ，满足 $a b c d = 9$ ，则 $a + b + c + d$ 的值为（）

A、0 B、4 C、10 D、无法确定

查看试题解析
3. 已知 $a b c > 0$ ，则式子： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} =$ （）

A、 $3$ B、 $3$ 或 $1$ C、 $3$ 或 $- 1$ D、 $3$ 或 $1$ 或 $- 1$

查看试题解析
4. 有理数a、b满足|a－b|=|a|+| b|，则a、b应满足的条件是（）

A、ab≥0 B、ab ＞1 C、ab ≤0 D、ab≤1

查看试题解析
5. 有理数 $a$ ， $b$ ， $c$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）

① $a b c < 0$ ；② $a - b + c < 0$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 3$ ；④ $| a - b | - | b + c | + | a - c | = 2 a$ .

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 九宫格起源于中国古代的神秘图案河图和洛书.如图，将 $3$ ， $2$ ， $1$ ， $0$ ， $- 1$ ， $- 2$ ， $- 3$ ， $- 4$ ， $- 5$ 填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则 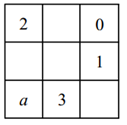$a$ 的值为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、 $- 5$

查看试题解析
7. 若abc≠0，则 $\frac{| a |}{a}$ ＋ $\frac{| b |}{b}$ + $\frac{c}{| c |}$ 的值为（）

A、±3或±1 B、±3或0或±1 C、±3或0 D、0或±1

查看试题解析
8. 若 $| a b c | = - a b c$ ，且 $a b c \neq 0$ ，则 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ 的值为（）

A、1或－3 B、－1或－3 C、±1或±3 D、无法判断

查看试题解析
9. 下列说法正确的有（）
① $| a - b | = a - b$ ,则 $a \geq b$ ；②数轴上到某点距离相等的两个点对应的数相等

③ $a b c < 0$ ,则 $\frac{a b}{| a b |} + \frac{b c}{| b c |} + \frac{a c}{| a c |} + \frac{| a b c |}{a b c} = \pm 2$ ；④ $| a + b | = | a - b |,$ 则 $b = 0$

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如果有4个不同的正整数 $a$ 、 $b$ 、 $c$ 、 $d$ 满足 $(2019 - a) (2019 - b) (2019 - c) (2019 - d) = 9$ ，那么 $a + b + c + d$ 的值为（）

A、0 B、9 C、8076 D、8090

查看试题解析

二、填空题

11. 若n＝ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ， abc＜0，则n的值为．

查看试题解析
12. 三个有理数 $a$ ， $b$ ， $c$ ， $a b c < 0$ ， $a + b + c > 0$ ．当 $x = \frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 时， $x^{19} - 92 x + 10$ 的值为．

查看试题解析

13. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

例如，十进制中16+10=26，用十六进制表示为10+A=1A；十进制中25-15=10，用十六进制表示为19−F=A．由上可知，在十六进制中B×D=（运算结果用十六进制表示）．

查看试题解析

14. 若a，b，c都不为0，则 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的值可能是．

查看试题解析
15. 已知abc≠0，且 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的最大值为m，最小值为n，则m+n＝.

查看试题解析

三、解答题

16. 已知三个有理数a，b，c的积是负数，它们的和是正数，当x= $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 时，求代数式： x²⁰¹⁹-2x+2的值.

查看试题解析
17. 有一种“算24”的游戏，其规则是：任取四个1～13之间的自然数，将这四个数（每数只能用一次）进行加减乘除混合运算，其结果为24.例如2，3，4，5作运算.（5+3－2）×4=24，现有四个有理数3、4、－6、10，运用以上规则写出等于24的算式，你能写出几种算法?

查看试题解析
18. 阅读下列内容，并完成相关问题：
小明说：“我定义了一种新的运算，叫❈（加乘）运算．”然后他写出了一些按照❈（加乘）运算的运算法则进行运算的算式：
（+4）❈（+2）=+6；（﹣4）❈（﹣3）=+7；
（﹣5）❈（+3）=﹣8；（+6）❈（﹣7）=﹣13；
（+8）❈0=8；0❈（﹣9）=9．
小亮看了这些算式后说：“我知道你定义的❈（加乘）运算的运算法则了．”
聪明的你也明白了吗？

(1)、归纳❈（加乘）运算的运算法则：
两数进行❈（加乘）运算时，．
特别地，0和任何数进行❈（加乘）运算，或任何数和0进行❈（加乘）运算，．

(2)、计算：[（﹣2）❈（+3）]❈[（﹣12）❈0]（括号的作用与它在有理数运算中的作用一致）

(3)、我们知道加法有交换律和结合律，这两种运算律在有理数的❈（加乘）运算中还适用吗？请你任选一个运算律，判断它在❈（加乘）运算中是否适用，并举例验证．（举一个例子即可）”

查看试题解析
19. 已知： $a b > 0$ ， $a + b < 0$ ， $a^{2} = 25$ ， $| b | = 2$ ，求 $a^{3} + b^{2} - a b$ 的值.

查看试题解析

四、综合题

20.

(1)、已知 $a ， b$ 互为相反数， $c ， d$ 互为倒数， $m$ 的绝对值是2，求 $\frac{a + b}{2 m_{}^{2} + 1} + 3 m_{}^{2} - 2 c d$ 的值；

(2)、若 $a ， b$ 在数轴上的位置如图所示，化简式子： $| a + b | - 2 | b - a | - | a |$ 。

查看试题解析
21. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答问题.
（提出问题）三个有理数a，b，c满足 $a b c > 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.

（解决问题）解：由题意，得a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①a，b，c都是正数，即 $a > 0$ ， $b > 0$ ， $c > 0$ 时，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$ ；

②当a，b，c中有一个为正数，另两个为负数时，不妨设 $a > 0$ ， $b < 0$ ， $c < 0$ ，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} =$ $\frac{a}{a} + \frac{- b}{b} + \frac{- c}{c} = 1 + (- 1) + (- 1) = - 1$ ，综上所述， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 值为3或−1.

（探究）请根据上面的解题思路解答下面的问题：

(1)、三个有理数a，b，c满足 $a b c < 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(2)、若a，b，c为三个不为0的有理数，且 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 1$ ，求 $\frac{a b c}{| a b c |}$ 的值.

查看试题解析
22. 有个补充运算符号的游戏：在“1□2□ $(- 6)$ □9”中的每个□内，填入+、-、×、÷中的某一个（可重复使用），然后计算结果．

(1)、计算： $1 + 2 - (- 6) - 9 =$ （直接写出结果）；

(2)、若 $1 \div 2 \times (- 6)$ □ $9 = 6$ ，请推算□内的符号应是什么？

(3)、请在□内填上×、÷中的一个，使计算更加简便，然后计算 $(1 \frac{3}{4} + \frac{7}{8} - \frac{7}{12})$ □ $(- \frac{7}{8})$

查看试题解析
23. 概念学习：
现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2写作2^③ ，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）写作（﹣3）^④ ，读作“（﹣3）的圈4次方”，一般地把 $\underset{n 个 a}{\underset{︸}{a \div a \div a \div \dots \div a}}$ （a≠0）写作a^ⓝ ，读作“a的圈n次方”．

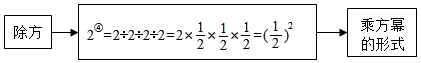
初步探究：

(1)、直接写出计算结果：3^②＝；（﹣ $\frac{1}{3}$ ）^③＝；

(2)、下列关于除方说法中，错误的有
A．任何非零数的圈2次方都等于1

B．任何非零数的圈3次方都等于它的倒数

C．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数

D．圈n次方等于它本身的数是1或﹣1．
深入思考：我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？

(3)、
比较：（﹣2）^⑩（﹣4）^⑩；（填“＞”“＜”或“＝”）

(4)、计算：﹣1^⑥+4²÷（﹣ $\frac{1}{2}$ ）^④×（﹣7）^③ ．

查看试题解析

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（培优卷）