（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（提升卷）

试卷更新日期：2023-07-08 类型：同步测试

进入出卷网下载

一、选择题

1. 已知数a，b在数轴上表示的点的位置如图所示，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a - b > 0$ C、 $- a > - b > a$ D、 $a \cdot b > 0$

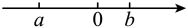查看试题解析
2. 实数 $a$ ， $b$ 在数轴上的位置如图所示，下列说法一定正确的是（）

A、 $a + b < 0$ B、 $| a | > | b |$ C、 $a - b > 0$ D、 $a b < 0$

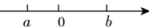查看试题解析
3. 已知有理数a，b在数轴上如图所示，则下列式子错误的是（）

A、 $a + b < 0$ B、 $\frac{a}{b} < 0$ C、 $| a | > | b |$ D、 $- a < b$

查看试题解析
4. 有理数a，b，c在数轴上对应的点的位置如图所示，其中 $| a | < | c |$ ，则下列各式：① $a b c > 0$ ；② $a - b + c < 0$ ；③ $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| c |}{c} = - 1$ ；④ $| a + b | - | b - c | + | a - c | = - 2 c$ ，正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 计算 $∣ - 2 \times 4 \times 0.25 ∣$ 的结果是（）

A、-4 B、-2 C、2 D、4

查看试题解析
6. 下列各式计算结果为负数的是（）

A、 $- 3 + 2$ B、 $2 - (- 3)$ C、 $3 \times 2$ D、 $(- 3) \div (- 2)$

查看试题解析
7. 在算式 $(- 1) □ (- 3)$ 的“□”内填上下列运算符号，使计算结果最大，这个符号是（）

A、+ B、- C、× D、÷

查看试题解析
8. 有理数 $a$ 、 $b$ 在数轴上的位置如图所示，则下列结论正确的是（）

A、 $\frac{a}{b} > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $a + b < 0$

查看试题解析
9. 有理数 $a$ ， $b$ 在数轴上对应的位置如图所示，则下列结论成立的是（）

A、 $a + b > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $\frac{a}{b} > 0$

查看试题解析
10. 给出下列等式：① $(- 1) \times (- 2) \times (- 3) = 6$ ；② $(- 36) \div (- 9) = - 4$ ；③ $\frac{2}{3} \times (- \frac{9}{4}) \div (- 1) = \frac{3}{2}$ ；④ $(- 4) \div$ $\frac{1}{2} \times (- 2) = 16$ ．其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 有理数 $a$ ， $b$ ， $c$ 在数轴上对应的点的位置如图所示，下列各式正确的是（填序号即可）.
① $a b c < 0$ ；② $a + c < 0$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 1$ ；④ $| c - b | + | a - b | = | a - c |$

查看试题解析
12. 已知 $| a | = 3$ ， $b = - 8$ ， $a b > 0$ ，则 $a - b$ 的值为．

查看试题解析
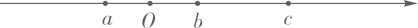13. 在2，-4，-5，6这四个数中，任取两个数相乘，所得的积最大是．

查看试题解析
14. 整数a、b、c满足1000|a|+10|b|+|c|=2023，其中|a|>1且abc>1，则a+b+c的最小值是．

查看试题解析
15. 若 $| x | = 3$ ， $| y | = 4$ 且 $x y < 0$ ，则 $\frac{y}{x} =$ ．

查看试题解析

三、解答题

16. 若a、b互为相反数，c、d互为倒数，m的绝对值为2.求 $m + c d + \frac{a + b}{m}$ 的值.

查看试题解析
17. 已知a，b互为相反数（a，b均不为0），m，n互为倒数，k是到原点距离为2的数，且 $k < 0$ .求代数式 $\frac{3 a}{b} - \frac{5}{m n} + 4 k$ 的值.

查看试题解析
18. 已知 $| a | = 3$ ， $| b | = 5$ ，且 $a > b$ ，求 $b - 2 a$ 的值.

查看试题解析
19. 已知a、b互为相反数，c、d互为倒数，m的倒数等于它本身，求 $| m | - \frac{c d}{m} + (a + b) m$ 的值．

查看试题解析

四、综合题

20. 如图，有5张写着不同的数字的卡片，请你按要求借助卡片上的数字完成下列各题：

(1)、从中取出2张卡片，使卡片上的2个数的和最小，则和的最小值是多少？

(2)、从中取出2张卡片，使卡片上的2个数相乘的积最小，则积的最小值是多少？

(3)、再制作一张写有数字的卡片，使6张卡片上数字之和为0，则新做的卡片上数字应写多少？

查看试题解析
21. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”.
【提出问题】三个有理数满足abc>0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.
【解决问题】解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.
①当a，b，c都是正数，即a>0，b>0，c>0时，则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$ ；
（备注：一个非零数除以它本身等于1，如：3 $\div$ 3=1，则 $\frac{a}{a} = 1 ， (a \neq 0)$ ）
②当a，b，c有一个为正数，另两个为负数时，设a>0，b<0，c<0，则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{- b}{b} + \frac{- c}{c} = 1 + (- 1) + (- 1) = - 1$ ，
$\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1.
【探究】请根据上面的解题思路解答下面的问题：

(1)、三个有理数a，b，c满足 $a b c < 0 ，$ 求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(2)、已知|a|=3，|b|=1，且a<b，求a-b的值.

查看试题解析
22. 根据实际规律我们知道：海拔高度每升高100米，气温将下降0.6℃．甲、乙两名登山运动员在攀登同一座高峰，途中甲发信息说他所在地的气温为5℃，海拔为1200米，同一时刻乙发回信息说他所在地气温为-4℃．（设地面海拔为0米）

(1)、求此刻地面的气温为多少℃；

(2)、求乙所在地的海拔高度．

查看试题解析
23. 薛老师坚持跑步锻炼身体，他以 $30 m i n$ 为基准，超过 $30 m i n$ 的部分计为“+”，不足 $30 m i n$ 的部分计为“-”，将连续7天的跑步时间（单位： $m i n$ ）记录如下：
星期
一
二
三
四
五
六
日
与30分钟差值
$+ 10$
$- 8$
$+ 12$
$- 6$
$+ 11$
$+ 14$
$- 3$

(1)、薛老师跑步时间最长的一天比最短的一天多跑几分钟？

(2)、若薛老师跑步的平均速度为 $0.1 k m / m i n$ ，请计算这七天他共跑了多少 $k m$ ？

查看试题解析

星期	一	二	三	四	五	六	日
与30分钟差值	$+ 10$	$- 8$	$+ 12$	$- 6$	$+ 11$	$+ 14$	$- 3$

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（提升卷）