浙江省杭州市拱墅区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有个选项是符合题目要求的.

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若代数式 $\sqrt{a - 1}$ 有意义，则a的取值范围是（）

A、a≥1 B、a＝1 C、a≤1 D、a≠1

查看试题解析
3. 若点（-3，2）在反比例函数 $y = \frac{k}{x} (k ≠ 0)$ 的图象上，则下列各点也在此函数图象上的是（）

A、（1，6） B、（-1，6） C、（-3，-2） D、（3，2）

查看试题解析
4. 方程 $\sqrt{3} x = \sqrt{6}$ 的解为（）

A、 $x = \frac{\sqrt{3}}{2}$ B、 $x = \frac{\sqrt{2}}{2}$ C、 $x = \sqrt{2}$ D、 $x = 2 \sqrt{3}$

查看试题解析
5. 关于x的方程x²-ax-2＝0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 若一组数据2，4，5，1，a的平均数为a，则a＝（）

A、1 B、2.4 C、2 D、3

查看试题解析
7. 设五边形的内角和为α，三角形的外角和为β，则（）

A、α＝β B、 $α ＝ \frac{3}{2} β$ C、α＝2β D、α＝3β

查看试题解析
8. 如图，在矩形ABCD中，以点D为圆心，AD为半径作弧与BD交于点E，以点B为圆心，AB为半径作弧与BD交于点F．设AB＝a，AD＝b，则（）

A、线段DF的长是方程x²+2ax＝b²的一个解 B、线段DF的长是方程x²-2ax＝b²的一个解 C、线段BE的长是方程x²+bx＝a²的一个解 D、线段BE的长是方程x²-bx＝a²的一个解

查看试题解析
9. 已知点R₁（a-2，b）与点P₂（a+1，b-2）在反比例函数 $y = \frac{k}{x} (k ≠ 0)$ 的图象上，（）

A、若k＞0，则a＞2，0＜b＜2 B、若k＞0，则a＜-1，b＞2 C、若k＜0，则a＜2，b＞2 D、若k＜0，则-1＜a＜2，0＜b＜2

查看试题解析
10. 如图，在正方形ABCD中，点F在边CD上（不与点C，点D重合），点E是CB延长线上的一点，且满足BE＝DF，连接EF，过点A作 AH⊥EF，垂足是点H，连接BH．设AB＝a，BE＝b，BH＝c，则（）

A、2c＝a+b B、 $\sqrt{2} c = a + b$ C、 $\sqrt{2} c = a - b$ D、2c²＝a²+b

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分.

11. 若关于x的方程x²-mx＝0的一个根是1，则m＝．

查看试题解析
12. 用一个x的值来说明“ $\sqrt{x^{2}} = x$ ”是错误的，则x的值可以是．

查看试题解析
13. 小方在本学期的数学平时成绩、期中成绩、期末成绩分别是90分、80分、95分，若平时成绩、期中成绩、期末成绩在学期成绩所占的比例分别为30%，30%，40%，则小方在本学期的数学成绩是分．

查看试题解析
14. 已知点O是平行四边形ABCD两条对角线的交点，AC＝12．BC＝18，OD＝14，则△OBC的周长为．

查看试题解析
15. 如图，在平面直角坐标系中，一次函数y＝x+b的图象与反比例函数 $y = \frac{k}{x} (k ≠ 0)$ 的图象交于 A（1，y₁）B（-3，y₂）．请根据图象写出不等式 $x > \frac{k}{x} - b$ 的解集．

查看试题解析
16. 如图是一张矩形纸片ABCD，点E在边BC上，且满足 AB＝2BE，把△ABE沿直线AE折叠，使点B落在点F处，EF的延长线与边CD交于点G．若CG＝DG，则 $\frac{C E}{B E}$ ＝．

查看试题解析

三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算步骤.

17. 计算：

(1)、 $(\sqrt{2} - \sqrt{3}) × \sqrt{2}$

(2)、 $(\sqrt{5})^{2} + \sqrt{12} × \sqrt{3}$ ．

查看试题解析
18. 解方程：

(1)、x²+x＝0；

(2)、4x²+1＝4x．

查看试题解析

19. 为确保让学生吃得放心，全力守护学生“舌尖”上的安全，区食品安全检测员随机抽取某两所学校，并对两所学校食堂菜品进行检测评分（满分10分），并将数据进行整理和分析成如下统计图和未完成的分析表．

A、B两校菜品评分情况分析表

学校	平均数	众数	中位数	方差
A校	8	8	b	d
B校	a	10	c	4.4

根据以上信息，回答下列问题：

(1)、求分析表中a，b，c，d的值．

(2)、根据上述统计量对两校的菜品作出评价，并简述理由．

查看试题解析

20. 如图，在四边形ABCD中，AB∥CD，AO＝CO．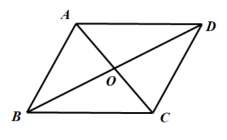

(1)、求证：四边形ABCD是平行四边形．

(2)、若CD＝3， $B D = 2 \sqrt{13}$ ， AC⊥AB，求四边形ABCD的面积．

查看试题解析
21. 五一假期，小王一家从杭州到温州自驾游，已知杭州到温州市区A处的路程为300千米，小王家的车油箱的容积为55升，小王把油箱加满后驾驶汽车从杭州出发．

(1)、求汽车行驶的总路程s（单位：千米）与平均耗油量b（单位：升/千米）的函数表达式．

(2)、小王以平均每千米耗油0.1升的速度驾驶汽车到达温州市区A处，休整后沿图示路线继续出发，先到雁荡山B处，再到楠溪江C处，最后到洞头D处．由于下雨，从A处开始直到D处小王降低了车速，此时平均每千米的耗油量增加了20%．如果小王始终以此速度行驶，不需加油能否到达洞头D处？如果不能，至少还需加多少油？

查看试题解析
22. 如图，在菱形ABCD中，60°＜∠ABC＜90°，点E在边BC上（不与点B，点C重合），线段EC的中垂线交对角线BD于点F，连接AE，AF，EF，CF．

(1)、求证：AF＝EF．

(2)、设∠ABC＝α，∠AEF＝β．圆圆同学通过画图和测量得到以下近似数据：
α
70
76
80
88
β
35
38
40
44
猜想：β关于α的函数表达式，并给出证明．

(3)、若AB＝AE，AB∥FE，求证：BF＝CF+CE．

查看试题解析

23. 根据以下素材，完成探索任务．

探索果园土地规划和销售利润问题
素材1	某农户承包了一块长方形果园ABCD，图1是果园的平面图，其中AB＝200米，BC＝300米．准备在它的四周铺设道路，上下两条横向道路的宽度都为2x米，左右两条纵向道路的宽度都为x米，中间部分种植水果．已知道路的路面造价是50元/m²；出于货车通行等因素的考虑，道路宽度不超过12米，且不小于5米．
素材2	该农户发现某一种草莓销售前景比较不错，经市场调查，草莓培育一年可产果，已知每平方米的草莓销售平均利润为100元；果园每年的承包费为25万元，期间需一次性投入33万元购进新苗，每年还需25万元的养护、施肥、运输等其余费用．
问题解决
任务1	解决果园中路面宽度的设计对种植面积的影响．	⑴请直接写出纵向道路宽度x的取值范围． ⑵若中间种植的面积是44800m² ，则路面设置的宽度是否符合要求．
任务2	解决果园种植的预期利润问题．（净利润＝草莓销售的总利润一路面造价费用一果园承包费用一新苗购置费用一其余费用，	⑶经过l年后，农户是否可以达到预期净利润400万元？请说明理由．

查看试题解析