(冀教版)2023-2024学年七年级数学上册2.8 平面图形的旋转 期中复习
试卷更新日期:2023-07-07 类型:复习试卷
一、选择题
-
1. 下列四张图形中,经过旋转之后不能得到的是( )A、
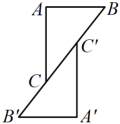 B、
B、 C、
C、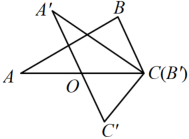 D、
D、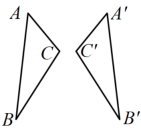 2. 如图,将三角形绕A逆时针旋转得到三角形 , 若 , , 则( )
2. 如图,将三角形绕A逆时针旋转得到三角形 , 若 , , 则( ) A、 B、 C、 D、3. 以长方形的一边为轴旋转一周,得到的立体图形为( )A、长方体 B、圆柱 C、圆锥 D、球4. 图2是由图1经过某一种图形的运动得到的,这种图形的运动是( )
A、 B、 C、 D、3. 以长方形的一边为轴旋转一周,得到的立体图形为( )A、长方体 B、圆柱 C、圆锥 D、球4. 图2是由图1经过某一种图形的运动得到的,这种图形的运动是( ) A、平移 B、翻折 C、旋转 D、以上三种都不对5. 如图,在方格纸中,将绕点按顺时针方向旋转90°后得到 , 则下列四个图形中正确的是( )
A、平移 B、翻折 C、旋转 D、以上三种都不对5. 如图,在方格纸中,将绕点按顺时针方向旋转90°后得到 , 则下列四个图形中正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,三角尺的顶点在直线上, . 现将三角尺绕点旋转,若旋转过程中顶点始终在直线的上方,设 , , 则下列说法中,正确的是( )
6. 如图,三角尺的顶点在直线上, . 现将三角尺绕点旋转,若旋转过程中顶点始终在直线的上方,设 , , 则下列说法中,正确的是( ) A、若 , 则 B、与一定互余 C、与有可能互补 D、若增大,则一定减小7. 如图,三角形中, , . 将绕点B逆时针旋转得到 , 使点C的对应点恰好落在边上,则的度数是( )
A、若 , 则 B、与一定互余 C、与有可能互补 D、若增大,则一定减小7. 如图,三角形中, , . 将绕点B逆时针旋转得到 , 使点C的对应点恰好落在边上,则的度数是( ) A、 B、 C、 D、8. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时 , 则( )
A、 B、 C、 D、8. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时 , 则( ) A、30° B、25° C、20° D、15°9. 如图,在三角形 中, ,将三角形 在平面内绕点A旋转到三角形 的位置,若 ,则旋转角的度数为( )
A、30° B、25° C、20° D、15°9. 如图,在三角形 中, ,将三角形 在平面内绕点A旋转到三角形 的位置,若 ,则旋转角的度数为( ) A、 B、 C、 D、10. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C'使各顶点仍在格点上,则其旋转角的度数是( )
A、 B、 C、 D、10. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C'使各顶点仍在格点上,则其旋转角的度数是( )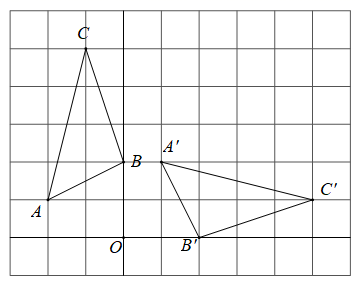 A、30° B、60° C、75° D、90°
A、30° B、60° C、75° D、90°二、填空题
-
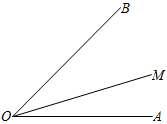
11. 如图,已知 , 射线从出发,以每秒的速度在内部绕点逆时针旋转,若和中,有一个角是另一个角的2倍,则运动时间为秒.
 12. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
12. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
 13. 一个三角板顶点B处刻度为“0”如图1,直角边落在数轴上,刻度“30”和“20”分别与数轴上表示数字-3和-1的点重合,现将该三角板绕着点B顺时针旋转90°,使得另一直角边落在数轴上,此时边上的刻度“15”与数轴上的点P重合,则点P表示的数是.
13. 一个三角板顶点B处刻度为“0”如图1,直角边落在数轴上,刻度“30”和“20”分别与数轴上表示数字-3和-1的点重合,现将该三角板绕着点B顺时针旋转90°,使得另一直角边落在数轴上,此时边上的刻度“15”与数轴上的点P重合,则点P表示的数是. 14. 将一张边长为8cm 的正方形纸片经过折叠、打开、画线得到如图1所示一副七巧板,再将图1沿实线分割,拼成如图2所示一个“家”的图形,该图形中的小正方形(阴影部分)的面积为cm2 .
14. 将一张边长为8cm 的正方形纸片经过折叠、打开、画线得到如图1所示一副七巧板,再将图1沿实线分割,拼成如图2所示一个“家”的图形,该图形中的小正方形(阴影部分)的面积为cm2 . 15. 如图,已知的三个角, , , , 将绕点顺时针旋转得到 , 如果 , 那么 .
15. 如图,已知的三个角, , , , 将绕点顺时针旋转得到 , 如果 , 那么 .
三、解答题
-
16. 在三角形 中, (如图),将三角形 绕着点 逆时针旋转得到三角形 (点 、 分别与点 、 对应),如果 与 的度数之比为 ,当旋转角大于 且小于 时,求旋转角的度数.
 17. 如图,用边长为1的正方形纸板制成一副七巧板,并将它拼成“小天鹅”图案,请你找出“小天鹅”图案中成135°的角,并用字母表示出来.
17. 如图,用边长为1的正方形纸板制成一副七巧板,并将它拼成“小天鹅”图案,请你找出“小天鹅”图案中成135°的角,并用字母表示出来.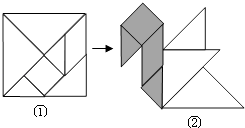 18. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.
18. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.
四、综合题
-
19. 含有 的直角三角板和含有的直角三角板按如图1放置,和重合.
 (1)、【操作一】三角板保持不动,将三角板绕着点B以每秒的速度按逆时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.
(1)、【操作一】三角板保持不动,将三角板绕着点B以每秒的速度按逆时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.①当时, ▲ 度.
②求t为何值时,.
(2)、【操作二】如图2,在三角板绕着点B以每秒的速度按逆时针方向旋转的同时,三角板也绕着点B以每秒的速度按逆时针方向旋转,设旋转时间为t秒.①求t为何值时,与重合.
②试探索:在两个三角板旋转的过程中,是否存在某个时刻,使得与中其中一个角是另一个角的两倍?若存在,请求出所有满足题意的t的值;若不存在,请说明理由.
20. 新定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图1,若射线 , 在的内部,且 , 则是的内半角.
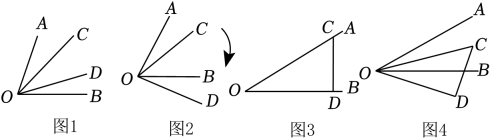
根据以上信息,解决下面的问题:
(1)、如图1, , , 若是的内半角,则 ;(2)、如图2,已知 , 将绕点按顺时针方向旋转一个角度()至.若是的内半角,求的值;(3)、把一块含有角的三角板按图3方式放置.使边与边重合,边与边重合.如图4,将三角板绕顶点以3度/秒的速度按顺时针方向旋转一周,旋转时间为秒,当射线、、、构成内半角时,直接写出的值.21. 如图1,摆放一副三角尺,使得点O在AB边上,将三角尺COD绕点O旋转. (1)、若∠AOD=0°,则∠COB= °;(2)、若∠AOD=45°,请在图2中画出∠COB;(3)、当∠AOD=α(0°<α<180°)时,求∠BOC的度数(结果可用α表示).22. 定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角,如图1,若 , 则是的内半角.
(1)、若∠AOD=0°,则∠COB= °;(2)、若∠AOD=45°,请在图2中画出∠COB;(3)、当∠AOD=α(0°<α<180°)时,求∠BOC的度数(结果可用α表示).22. 定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角,如图1,若 , 则是的内半角.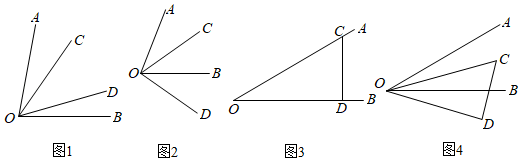 (1)、如图1, , , 是的内半角,则;(2)、如图2,已知 , 将绕点按顺时针方向旋转一个角度得 , 当旋转的角度为何值时,是的内半角;(3)、已知 , 把一块含有角的三角板如图3叠放,将三角板绕顶点以3度秒的速度按顺时针方向旋转(如图 , 问:在旋转一周的过程中,射线、、、能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.
(1)、如图1, , , 是的内半角,则;(2)、如图2,已知 , 将绕点按顺时针方向旋转一个角度得 , 当旋转的角度为何值时,是的内半角;(3)、已知 , 把一块含有角的三角板如图3叠放,将三角板绕顶点以3度秒的速度按顺时针方向旋转(如图 , 问:在旋转一周的过程中,射线、、、能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.