河南省驻马店市确山县2022-2023学年八年级下册数学期末考试试卷
试卷更新日期:2023-07-07 类型:期末考试
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
-
1. 在下列四组数中,属于勾股数的是( )A、0.3,0.4,0.5 B、9,40,41 C、6,7,8 D、1, ,2. 已知是整数,正整数n的最小值为( )A、2 B、0 C、3 D、43. 某手表厂抽查了10只手表的日走时误差,数据如下表所示(单位: ):
日走时误差
0
1
2
3
只数
3
4
2
1
则这10只手表的平均日走时误差(单位:s)是( )
A、0 B、0.6 C、0.8 D、1.14. 在中,对角线 , 相交于点O, , , 则边的长度x的取值范围是( )A、 B、 C、 D、5. 下列不能表示y是x的函数的是( )A、
B、x 0 5 10 15 y 3 3.5 4 4.5  C、
C、 D、
6. 一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒)。则这组数据的中位数为( )
D、
6. 一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒)。则这组数据的中位数为( ) A、36 B、34 C、32 D、377. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图2的图形,并测得 , 在此变化过程中结论错误的是( )
A、36 B、34 C、32 D、377. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图2的图形,并测得 , 在此变化过程中结论错误的是( )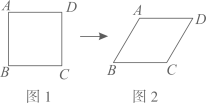 A、长度不变,为 B、长度变小,减少 C、面积变小,减少 D、长度变大,增大8. 对于一次函数(k,b为常数,)下表中给出5组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A、长度不变,为 B、长度变小,减少 C、面积变小,减少 D、长度变大,增大8. 对于一次函数(k,b为常数,)下表中给出5组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )0
1
2
3
2
5
8
12
14
A、2 B、5 C、8 D、129. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米10. 将盛有凉牛奶的瓶子放在热水中(如图甲所示),通过热传递方式改变牛奶的内能,图乙是凉牛奶与热水的温度随时间变化的图像.假设热水放出热量全部被牛奶吸收,下列回答错误的是( ) A、0~8min时,热水的温度随时间的增加逐渐降低; B、0~8min时,凉牛奶的温度随时间的增加逐渐上升; C、8min时,热水和凉牛奶的温度相同; D、0min时,两者的温度差为 .
A、0~8min时,热水的温度随时间的增加逐渐降低; B、0~8min时,凉牛奶的温度随时间的增加逐渐上升; C、8min时,热水和凉牛奶的温度相同; D、0min时,两者的温度差为 .二、填空题(每小题3分,共15分)
-
11. 计算3 的结果是.12. 请你写出一个点的坐标,它在第一象限,且在直线上,这个点可以为(写出一个即可).13. 2022年9月起,劳动课正式成为中小学的一门独立课程.某班为了选拔一名学生参加学校组织的以“热爱劳动励心智,品味生活促成长”为主题的展示活动,在班里组织了6项活动,分别是煮饭烧菜、收纳物品、种植植物、修理家电、打扫卫生、和面蒸馍.其中甲、乙两名学生较为突出,他们在6项活动中的成绩(单位:分)如表所示:
甲
12.1
12.1
12.0
11.9
11.8
12.1
乙
12.2
12.0
11.8
12.0
12.3
11.7
由于甲、乙两名学生成绩的平均数相同,班级决定依据他们成绩的稳定性进行选拔,那么被选中的是同学.
14. 数学家笛卡尔在《几何》一书阐述了坐标几何思想,主张取代数和几何中最好的东西以长补短.如右图,在直角坐标系中,矩形 , 点B的坐标是 , 则的长是 .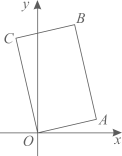 15. 已知a,b,c分别是的三条边长,c为斜边长, , 我们把关于x的形如的一次函数称为“勾股一次函数”.若点在“勾股一次函数”的图象上,且的面积是2,则c的值是 .
15. 已知a,b,c分别是的三条边长,c为斜边长, , 我们把关于x的形如的一次函数称为“勾股一次函数”.若点在“勾股一次函数”的图象上,且的面积是2,则c的值是 .三、解答题(本大题共8个小题,满分75分)
-
16. 计算(1)、;(2)、 .17. 如图,在的正方形网格中,每个小正方形的边长都为1,每个小正方形的顶点称为格点,及边上的点D均为格点.
 (1)、直接写出的面积为;(2)、用无刻度的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示.作出的角平分线;18. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形是平行四边形,对角线、相交于点O,点E、F在上, ▲ (填写序号).求证: .
(1)、直接写出的面积为;(2)、用无刻度的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示.作出的角平分线;18. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形是平行四边形,对角线、相交于点O,点E、F在上, ▲ (填写序号).求证: .注:如果选择多个条件分别解答,按第一个解答计分.
 19. “儿童散学归来早,忙趁东风放纸鸢.”如图,小明站在C处,同时小亮在斜坡的D处,且米,米, . (不考虑两人身高,点G、C、B在同一水平线上)
19. “儿童散学归来早,忙趁东风放纸鸢.”如图,小明站在C处,同时小亮在斜坡的D处,且米,米, . (不考虑两人身高,点G、C、B在同一水平线上) (1)、求小明与小亮之间的距离 .(2)、若风筝A在小明的北偏东45方向上,且高度为30米, , 求此时风筝A到小亮的距离 .20. 如今,绿道骑行已经成为市民的一种低碳生活新风尚.一辆单车,三五好友,或骑行于三里河河畔,或穿梭至盘龙山绿道,在蓝天碧水、绿树成荫中享受骑行魅力.城市骑行,不仅可以锻炼身体,享受户外,还可以发现更多城市美好.甲、乙两人相约8:20从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示.
(1)、求小明与小亮之间的距离 .(2)、若风筝A在小明的北偏东45方向上,且高度为30米, , 求此时风筝A到小亮的距离 .20. 如今,绿道骑行已经成为市民的一种低碳生活新风尚.一辆单车,三五好友,或骑行于三里河河畔,或穿梭至盘龙山绿道,在蓝天碧水、绿树成荫中享受骑行魅力.城市骑行,不仅可以锻炼身体,享受户外,还可以发现更多城市美好.甲、乙两人相约8:20从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示.
 (1)、直接写出当和时,s与t之间的函数表达式;(2)、通过计算说明,何时乙骑行在甲的前面?21. 为了让师生更规范地操作教室里的一体机设备,学校信息中心制作了“教室一体机设备培训”视频,并在视频课时间进行播放.结束后为了解初一、初二各班一体机管理员对设备操作知识的掌握程度,信息中心对他们进行了相关的知识测试现从初一、初二年级各随机抽取了15名一体机管理员的成绩,得分用x表示,共分成4组:A: , B: , C: , D: , 对得分进行整理分析,给出了下面部分信息:
(1)、直接写出当和时,s与t之间的函数表达式;(2)、通过计算说明,何时乙骑行在甲的前面?21. 为了让师生更规范地操作教室里的一体机设备,学校信息中心制作了“教室一体机设备培训”视频,并在视频课时间进行播放.结束后为了解初一、初二各班一体机管理员对设备操作知识的掌握程度,信息中心对他们进行了相关的知识测试现从初一、初二年级各随机抽取了15名一体机管理员的成绩,得分用x表示,共分成4组:A: , B: , C: , D: , 对得分进行整理分析,给出了下面部分信息:

初一年级一体机管理员的测试成绩在C组中的数据为:85,81,88.
初二年级一体机管理员的测试成绩:71,76,81,82,83,86,86,88,89,90,93,95,100,100,100.
成绩统计表如表:
(注:极差为样本中最大数据与最小数据差)
年级
平均数
中位数
最高分
众数
极差
初一
88
a
98
98
32
初二
88
88
100
b
c
(1)、 , , ;(2)、通过以上数据分析,你认为哪个年级的一体机管理员对一体机设备操作的知识掌握更好?并说明理由(写出一条理由即可).22. 科学家实验发现,声音在不同气温下传播的速度不同,声音在空气中的传播速度随温度的变化而有规律的变化.某兴趣小组为探究空气的温度与声音在空气中传播的速度y(米/秒)之间的关系,在标准实验室里进行了多次实验.如表为实验时记录的一些数据.温度
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
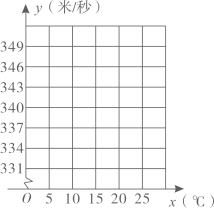 (1)、在如图的平面直角坐标系中,横轴为气温 , 纵轴为声音在空气中传播的速度y(米/秒),描出以表格中数据为坐标的各点;(2)、观察所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由;(3)、当气温是时,求声音在空气中传播的速度;23. 综合与实践
(1)、在如图的平面直角坐标系中,横轴为气温 , 纵轴为声音在空气中传播的速度y(米/秒),描出以表格中数据为坐标的各点;(2)、观察所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由;(3)、当气温是时,求声音在空气中传播的速度;23. 综合与实践综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
 (1)、操作判断
(1)、操作判断操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板沿方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
①图1中四边形的形状是;
②图2中与的数量关系是;四边形的形状是 .
(2)、迁移探究小航将一副等腰直角三角板换成一副含角的直角三角板,继续探究,已知三角板边长为 , 过程如下:
将三角板按(1)中的方式操作,如图3,在平移过程中,四边形的形状能否是菱形,若不能,请说明理由,若能,请求出的长.
(3)、拓展应用在(2)的探究过程中;
当为等腰三角形时,请直接写出的长;