浙江省宁波市南山县2022-2023学年七年级下册数学期末考试试卷

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分.在每小题给出的四个选项中，只有一项符合题目要求）

1. “水是生命之源，滋润着世间万物”国家节水标志由水滴，手掌和地球变形而成．寓意：像对待掌上明珠一样，珍惜每一滴水!以下通过平移节水标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，是二元一次方程的是（）

A、 $3 x + y = 0$ B、 $x y - y = 0$ C、 $x - 2 y = z$ D、 $\frac{1}{x} + y = 0$

查看试题解析
3. 神舟十五号飞船于2022年11月29日发射成功，飞船搭载一种高控制芯片探针面积为0.0000162平方厘米，0.0000162用科学记数法表示为（）

A、 $0.162 \times 1 0^{- 7}$ B、 $1.62 \times 1 0^{- 6}$ C、 $1.62 \times 1 0^{- 5}$ D、 $16.2 \times 1 0^{- 4}$

查看试题解析
4. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 $(2 a)^{3} = 6 a^{3}$ D、 ${(a^{2} b)}^{3} = a^{2} b^{3}$

查看试题解析
5. 为了解宁波市七年级学生的视力情况，从中随机调查了500名学生的视力，下列说法正确的是（）

A、宁波市七年级学生是总体 B、每一名七年级学生是个体 C、500名七年级学生是总体的一个样本 D、样本容量是500

查看试题解析
6. 如图，下列说法错误的是（）

A、 $∠ 1$ 与 $∠ 2$ 是内错角 B、 $∠ 2$ 与 $∠ 3$ 是同位角 C、 $∠ 1$ 与 $∠ 3$ 是内错角 D、 $∠ 2$ 与 $∠ 4$ 是同旁内角

查看试题解析
7. 下列各式从左向右的变形中，是因式分解的为（）

A、 $2 x (x - 3) = 2 x^{2} - 6 x$ B、 $(x - 1) (x + 1) = x^{2} - 1$ C、 $4 x^{2} - 4 x + 1 = (2 x - 1)^{2}$ D、 $x^{2} + 2 x + 4 = (x + 1)^{2}$

查看试题解析
8. 若关于x的分式方程 $\frac{x - 1}{x + 1} = \frac{a}{x + 1} - 2$ 有增根，则a的值是（）

A、－2 B、－1 C、0 D、1

查看试题解析
9. 《九章算术》是人类科学史上应用数学的“算径之首“，书中记载：今有三人共车，二车空；二人共车，九人步.问：人与车各几何？译文：若3人坐一辆车，则两辆车是空；若2人坐一辆车，则9人需要步行；问：人与车各多少？设x辆车，人数为y人，根据题意可列方程组为（）

A、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x + 9 \end{array}$ B、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x - 9 \end{array}$ C、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x + 9 \end{array}$ D、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x - 9 \end{array}$

查看试题解析
10. 在长方形ABCD内，将一张边长为a的正方形纸片和两张边长为b的正方形纸片（ $a > b$ ），按图1，图2两种方式放置（两个图中均有重叠部分），矩形中未被这三张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $s_{1}$ ，图2中阴影部分的面积为 $s_{2}$ ，当 $A D - A B = 2$ 时，若知道下列条件，能求 $s_{1} - s_{2}$ 值的是（）

A、边长为a的正方形的面积 B、边长为b的正方形的面积 C、边长为a的正方形的面积与两个边长为b的正方形的面积之和 D、边长a与b之差

查看试题解析

二、填空题（每小题4分，共24分）

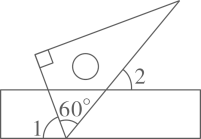
11. 使分式 $\frac{1}{x - 4}$ 有意义的x的取值范围是.

查看试题解析
12. 将数据73，75，77，79，74，75，76，72，71，78分组，72.5~74.5这一组的频率是.

查看试题解析
13. 请你写出一个解为 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ 的二元一次方程组：.

查看试题解析
14. 如图所示，将直尺与含 $60 °$ 角的直角三角板叠放在一起，若 $∠ 1 = 70 °$ ，则 $∠ 2$ 的度数为.

查看试题解析
15. 定义一种新运算，已知 $a \neq b$ ，当 $a > b$ 时， $a * b = \frac{a b}{a - b}$ ；当 $a < b$ 时， $a * b = \frac{a b}{b - a}$ ，若 $3 * x = 4$ ，则 $x =$ .

查看试题解析
16. 我国南宋数学家杨辉用“三角形”解释二项和的乘方规律，称之为“杨辉三角”，这个“三角形”给出了 $(a + b)^{n} (n = 1 ， 2 ， 3 ， 4 ， ⋯)$ 的展开式的系数规律（按n的次数由大到小的顺序）.
11 $(a + b)^{1} = a + b$
121 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$
1331 $(a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$
14641 $(a + b)^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$
…
请依据上述规律，写出 ${(x - \frac{1}{x})}^{2023}$ 展开式中含 $x^{2021}$ 项的系数是.

查看试题解析

三、解答题（本大题有8小题，共66分）

17. 计算：

(1)、 $(- 1)^{2} + 3^{- 2} - (2 \sqrt{3} - 1)^{0}$

(2)、 $(x + 2) (x - 2) + (4 x^{3} - x) \div x$

查看试题解析
18. 因式分解：

(1)、2a³-8a

(2)、 ${(x - 1)}^{2} + x - 1$

查看试题解析
19. 解方程：

(1)、 ${\begin{array}{l} x - y = 2 \\ x + 2 y = 5 \end{array}$

(2)、 $\frac{4}{1 - y} = \frac{2 y}{y - 1} + 1$

查看试题解析
20. 化简代数式 $(\frac{x^{2} + 1}{x} - 2) \div \frac{x - 1}{x^{2}}$ ，并求当 $x = 3$ 时代数式的值.

查看试题解析
21. 某校积极开展“阳光体育”活动，共开设了跳绳、足球、篮球、跑步四种运动项目，为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）.

(1)、求本次被调查的学生人数；

(2)、补全条形统计图；

(3)、喜爱篮球项目的学生人数所对应的扇形圆心角为度.

(4)、该校共有1600名学生，请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少？

查看试题解析
22. 如图， $A D ⊥ B E$ ， $B C ⊥ B E$ ， $∠ A = ∠ C$ ，点C，D，E在同一条直线上.

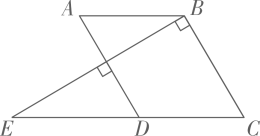(1)、请说明AB与CD平行.

(2)、若 $∠ A B C = 110 °$ ，求 $∠ E$ 的度数.

查看试题解析
23. 为了迎接在杭州举行的第19届亚运会，某旅游商店购进若干吉祥物钥匙扣和明信片，已知吉祥物钥匙扣的进价为20元/个，明信片的进价为5元/套.一个吉祥物钥匙扣的售价比一套明信片的售价高20元.若顾客花180元购买的吉祥物钥匙扣数量与花60元购买的明信片数量相同.

(1)、求吉祥物钥匙扣和明信片的售价.

(2)、为了促销，商店对吉祥物钥匙扣进行9折销售.某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件，商家获毛利润100元，请问有几种购买方案.

查看试题解析
24. 若一个整数能表示成 $a^{2} + b^{2}$ （a，b是整数）的形式，则称这个数为“完美数”.例如， $13 = 3^{2} + 2^{2}$ ，所以13是“完美数”，再如， $M = x^{2} + 2 x y + 2 y^{2} = (x + y)^{2} + y^{2}$ （x，y是整数），所以M也是“完美数”.

(1)、请直接写出一个小于10的“完美数”，这个“完美数”是；
判断：45（请填写“是”或“不是”）“完美数”；

(2)、已知 $S = x^{2} + 4 y^{2} - 6 x + 4 y + k$ （x，y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由.

(3)、如果数m，n都是“完美数”， $m \neq n$ ，试说明 $\frac{(m + n)^{2} - (m - n)^{2}}{4}$ 也是“完美数”.

查看试题解析