浙江省宁波市南山县2022-2023学年八年级下册数学期末考试试卷

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. 若式子 $\sqrt{x - 1}$ 有意义，则x的值可以为（）

A、4 B、－4 C、－1 D、0

查看试题解析
2. 下列航天图标，其文字上方的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列方程一定是一元二次方程的是（）

A、 $2 x - 1 = 4 x + 3$ B、 $2 x^{2} + y - 1 = 0$ C、 $2 x^{2} - 1 = 3$ D、 $a x^{2} + b x + c = 0$

查看试题解析
4. 用反证法证明：“在同一平面内，若 $a ⊥ b$ ， $c ⊥ b$ ，则 $a ∥ c$ ”时，首先应假设（）

A、 $a ∥ b$ B、 $c ∥ b$ C、a与b相交 D、a与c相交

查看试题解析
5. 菱形具有而矩形不一定具有的性质是（）

A、对角相等 B、邻角互补 C、对角线互相平分 D、对角线平分一组对角

查看试题解析
6. 若一元二次方程 $x^{2} - 2 x + k = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、 $k > 1$ B、 $k < 1$ C、 $k < 1$ 且 $k \neq 0$ D、 $k \geq 1$

查看试题解析
7. 一场有19位同学参加的比赛，取前10名进决赛且所得分数互不相同.某同学知道自己的分数后要判断是否能进决赛，他只需要知道这19位同学所得分数的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
8. 以下函数值在自变量的取值范围内随着自变量的增大而减小的是（）

A、 $y = 2 x - 1$ B、 $y = \frac{1}{3} x$ C、 $y = - \frac{3}{x} (x < 0)$ D、 $y = \frac{6}{x} (x > 0)$

查看试题解析
9. 高空抛物极其危险，是我们必须杜绝的行为.据研究，高空抛出的物体下落的时间t（单位：s）和高度h（单位：m）近似满足 $t = \sqrt{\frac{h}{5}}$ （不考虑风速的影响）.从20m，40m高空抛物到落地所需时间分别为 $t_{1}$ ， $t_{2}$ ，则 $t_{2}$ 是 $t_{1}$ 的（）

A、2倍 B、 $\sqrt{2}$ 倍 C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
10. 如图，在 $▱ A B C D$ 中，以BC和AD为斜边分别向内作等腰 $R t △ B C E$ 和等腰 $R t △ A D G$ ，延长BE和DG分别交AG和CE于点H和F，直线FH分别交AD和BC于点I和J.若四边形EFGH是正方形， $▱ A B C D$ 的面积为S，下列哪条线段的长度不能用S来表示（）

A、AB B、BC C、CE D、IJ

查看试题解析

二、填空题（本大题共6小题，共24分）

11. 已知一组数据的方差是4，那么这组数据的标准差是.

查看试题解析
12. 若 $x$ ＜2，化简 $\sqrt{{(x - 2)}^{2}} =$

查看试题解析
13. 将方程 $x^{2} - 6 x - 5 = 0$ 整理成 ${(k x + p)}^{2} = q$ 的形式为.

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 4$ ， CM是斜边AB上的中线，点N是BC边上一点，点D，E分别为CN，MN的中点，则DE的值是.

查看试题解析
15. 如图，将长宽比为 $3 ： 2$ 的矩形ABCD沿着EF折叠，使点C落到宽AD上点 $C^{'}$ 处，点B落到点 $B^{'}$ 处，且满足 $A C^{'} = C^{'} F$ ，则 $\frac{A C^{'}}{A D} =$ .

查看试题解析
16. 如图，在平面直角坐标系xOy中，正方形ABCD的顶点A、C恰好落在双曲线 $y = \frac{2 \sqrt{2}}{x}$ 上，且点O在AC上，AD交x轴于点E.①当A点坐标为 $(1 ， m)$ 时，D点的坐标为；②当CE平分 $∠ A C D$ 时，正方形ABCD的面积为.

查看试题解析

三、解答题（本大题共8小题，共66分）

17. 计算：

(1)、 $\sqrt{12} + (2 - \sqrt{3})^{2}$

(2)、 $\sqrt{6} \div \sqrt{3} - \frac{1}{\sqrt{3} - \sqrt{2}}$

查看试题解析
18. 解下列方程：

(1)、 ${(x - 4)}^{2} = 9$

(2)、 $2 x^{2} - 5 x + 3 = 0$

查看试题解析
19. 某学校从八年级学生中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试，根据测试成绩绘制出统计表和统计图.
甲组成绩统计表

成绩/分

7

8

9

10

人数/人

1

9

5

5

(1)、 $m =$ ，甲组成绩的众数乙组成绩的众数（填“＞”“＜”或“＝”）.

(2)、求甲组的平均成绩.

(3)、计算出甲组成绩的方差为0.81，乙组成绩的方差为0.75，则成绩更加稳定的是组（填“甲”或“乙”）.

查看试题解析
20. 如图，某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成，该装置竖直放置时，活塞受到托盘中重物的压力向下压缩装置内的空气.某同学试着放上不同质量的物体，并根据筒侧的刻度记录活塞到筒底的距离，得到下面5组数据：
重物质量m/kg
2
3
4
6
8
活塞到桶底的距离h/cm
24
16
12
8
6

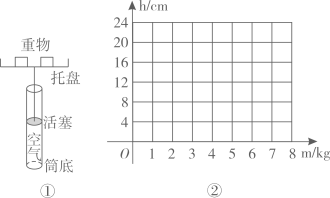(1)、以表中各组数据对应值为点的坐标，在如图直角坐标系中描出相应的点并用光滑的曲线连结.

(2)、能否用学过的函数刻画变量h和m之间的关系？如果能，请求出h关于m的解析式；如果不能，请说明理由.

(3)、要使活塞到筒底的距离大于5，请直接写出在托盘中放入重物的质量m的取值范围.

查看试题解析
21. 如图，已知点E是 $▱ A B C D$ 的边DC延长线上的一个点， $C E = D C$ .连接AE，交BC于点F，连接AC，BE.

(1)、求证：四边形ABEC是平行四边形.

(2)、若 $A E = A D$ ，请判断四边形ABEC的形状并说明理由.

查看试题解析
22. 新能源汽车已逐渐成为人们的交通工具.某品牌新能源汽车经销商对新上市的A汽车在1月份至3月份的销售情况进行统计，发现A汽车1月份的销量为20辆，3月份的销量为45辆.

(1)、求A汽车销量的月平均增长率.

(2)、为了扩大A汽车的市场占有量，提升A汽车的销售业绩，该公司决定采取适当的降价措施（降价幅度不超过售价的10%）.经调查发现，当A汽车的销售单价定为12万元时，平均每月的售量为30辆，在此基础上，若A汽车的销售单价每降1万元，平均每月可多售出10辆，若销售额要达到440万元，则每辆A汽车需降价多少万元？

查看试题解析
23. 阅读材料，根据上述材料解决以下问题：
材料1：若一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ .
材料2：已知实数m，n满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，则m，n是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根.

(1)、材料理解：一元二次方程 $3 x^{2} - 6 x + 1 = 0$ 两个根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} =$ ， $x_{1} x_{2} =$ .

(2)、应用探究：已知实数m，n满足 $9 m^{2} - 9 m - 1 = 0$ ， $9 n^{2} - 9 n - 1 = 0$ ，且 $m \neq n$ ，求 $m^{2} n + m n^{2}$ 的值.

(3)、思维拓展：已知实数s、t分别满足 $9 s^{2} + 9 s + 1 = 0$ ， $t^{2} + 9 t + 9 = 0$ ，其中 $s t \neq 1$ 且 $s t \neq 0$ .求 $\frac{3 s t + 9 s + 3}{t}$ 的值.

查看试题解析
24. 定义：把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.

(1)、矩形勾股四边形（填“是”或“不是”）.

(2)、如图在直角坐标系xOy中，直线 $y = - x + 1$ 与双曲线 $y = \frac{- 6}{x}$ 相交于A，B两点，点 $P (- 3 ， 0)$ 在x轴负半轴上，Q为直角坐标平面上一点.
①分别求出A、B两点的坐标.
②当四边形APQB是平行四边形时，如图（1），请证明 $▱ A P Q B$ 是勾股四边形.

(3)、在（2）的条件下，当以A、B、P、Q为顶点的四边形是勾股四边形时，请直接写出Q点的坐标.

查看试题解析

成绩/分	7	8	9	10
人数/人	1	9	5	5

重物质量m/kg	2	3	4	6	8
活塞到桶底的距离h/cm	24	16	12	8	6