江苏省泰州市姜堰区2022-2023学年八年级下册数学期末考试试卷
试卷更新日期:2023-07-07 类型:期末考试
一、选择题(本大题共有6小题,每小题3分,共18分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、3. 下列调查中,适宜采用普查的是( )A、查找某书本中的印刷错误 B、检测一批灯泡的使用寿命 C、了解公民保护环境的意识 D、了解长江中现有鱼的种类4. 若是方程的根,则的值为( )A、 B、 C、 D、5. 要使分式的值扩大4倍,的取值可以如何变化( )A、的值不变,的值扩大4倍 B、的值不变,的值扩大4倍 C、的值都扩大2倍 D、的值都扩大4倍6. 如图,菱形的边长为 , 点在轴正半轴上,反比例函数的图像经过点和线段的中点 , 且点的横坐标为 , 则与满足的关系为( )
2. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、3. 下列调查中,适宜采用普查的是( )A、查找某书本中的印刷错误 B、检测一批灯泡的使用寿命 C、了解公民保护环境的意识 D、了解长江中现有鱼的种类4. 若是方程的根,则的值为( )A、 B、 C、 D、5. 要使分式的值扩大4倍,的取值可以如何变化( )A、的值不变,的值扩大4倍 B、的值不变,的值扩大4倍 C、的值都扩大2倍 D、的值都扩大4倍6. 如图,菱形的边长为 , 点在轴正半轴上,反比例函数的图像经过点和线段的中点 , 且点的横坐标为 , 则与满足的关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共有10小题,每小题3分,共30分.请把答案直接填写在答题卡相应位置上)
-
7. 若二次根式在实数范围内有意义,则的取值范围是 .8. 分式和的最简公分母为 .9. 如图,一粒杂质从粗细相同且水平放置的“田字型”水管的进水口流入,在三处装有过滤网,该杂质经过处过滤网的可能性最大.
 10. 如图,在平行四边形中,对角线相交于点 , 则 .
10. 如图,在平行四边形中,对角线相交于点 , 则 .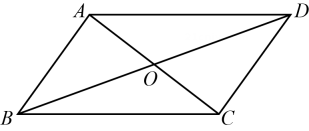 11. 实数满足 , 则的值为 .12. 若 , 则 .13. 如图,点在反比例函数的图像上,过点作轴的平行线 . 已知点坐标为 , 结合函数图象可知,当时,的取值范围是 .
11. 实数满足 , 则的值为 .12. 若 , 则 .13. 如图,点在反比例函数的图像上,过点作轴的平行线 . 已知点坐标为 , 结合函数图象可知,当时,的取值范围是 . 14. 若和是一元二次方程的两个实数根,则 .15. 在四边形中,点分别为的中点,则 . (选填“>”、“<”、“=”、“≥”或“≤”)16. 如图,一次函数与反比例函数的图像相交于两点,且点的横坐标为1,该反比例函数的图象关于直线对称后的图像经过直线上的点 , 则线段的长度为 .
14. 若和是一元二次方程的两个实数根,则 .15. 在四边形中,点分别为的中点,则 . (选填“>”、“<”、“=”、“≥”或“≤”)16. 如图,一次函数与反比例函数的图像相交于两点,且点的横坐标为1,该反比例函数的图象关于直线对称后的图像经过直线上的点 , 则线段的长度为 .
三、解答题(本大题共10小题,共102分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
-
17.(1)、计算:(2)、化简:18. 解方程:(1)、(2)、19. 某校为了解本校学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了如图两幅不完整的统计图:

请根据以上统计图的信息,完成下列问题:
(1)、抽取的样本容量为;(2)、补全条形统计图,并求出扇形统计图中“羽毛球”运动所对应的圆心角的度数;(3)、该校共有2000名学生,请估计该校喜欢足球运动的人数.20. 已知:如图,是正方形对角线上的一点,且 , 垂足为 , 交于点 .
求证: .
21. 问题:“某工程队准备修建一条长3000米的下水管道,由于采用新的施工方式, ▲ , 提前2天完成任务,求原计划每天修建下水管道的长度?”条件:⑴实际每天修建的长度比原计划多;
⑵原计划每天修建的长度比实际少75米.
在上述的2个条件中选择1个(仅填序号)补充在问题的横线上,并完成解答.
22. 已知代数式 .(1)、当为何值时,代数式比的值大2;(2)、求证:对于任意的值,代数式的值恒为正数.23. 如图,矩形纸片 , 点为边上一动点,将矩形纸片沿折叠,折叠后与相交于点 . (1)、为何值时,点与点重合;(2)、当长为何值时,的面积最大?并求出面积的最大值.24. 如图,某可调节亮度的台灯,可通过调节台灯的电阻,控制电流的变化实现亮度的调节.该台灯电流与电阻的反比例函数图象过点 .
(1)、为何值时,点与点重合;(2)、当长为何值时,的面积最大?并求出面积的最大值.24. 如图,某可调节亮度的台灯,可通过调节台灯的电阻,控制电流的变化实现亮度的调节.该台灯电流与电阻的反比例函数图象过点 . (1)、求电流与电阻的函数表达式;(2)、若该台灯工作的最小电流为 , 最大电流为 , 则该台灯的电阻的取值范围是?25.
(1)、求电流与电阻的函数表达式;(2)、若该台灯工作的最小电流为 , 最大电流为 , 则该台灯的电阻的取值范围是?25. (1)、【问题探究】
(1)、【问题探究】构造多边形比较无理数大小:在图25-1的正方形方格纸中(每个小正方形的边长都为1),线段的长度为 , 线段的长度为 .
①请结合图25-1,试说明;
②在图25-2中,请尝试构造三角形,比较与的大小;
③在图25-3中,请尝试构造四边形,比较与的大小;
(2)、【迁移运用】如图25-4,线段为线段上的任意一点,设线段 . 则是否有最小值?如果有,请求出最小值,并仅用无刻度的直尺在图中标出取最小值时点的位置;如果没有,请说明理由.
26. 如图,点为反比例函数的图像上一点,且点的横坐标为 , 过点作轴、轴的平行线,分别交反比例函数的图像于、 , 过点作轴的平行线,交反比例函数的图像于 , 连接 . (1)、当时,求线段的长;(2)、若;
(1)、当时,求线段的长;(2)、若;①若 , 求的值;
②求的值;
(3)、当的值一定时,四边形的面积是否随的变化而变化?若不变,请用含的代数式表示四边形的面积;若变化,请说明理由.