河南省驻马店市上蔡县2022-2023学年七年级下册数学期末考试试卷

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、选择题（本大题包括10小题，每小题3分，共30分）

1. x取下列各数时，能使不等式 $x + 1 < 2$ 成立的x的值是（）

A、0 B、1 C、2 D、3

查看试题解析
2. 已知三角形的两边长分别是3cm和8cm，则下列长度的四条线段中能作为第三边的是（）

A、3cm B、5cm C、8cm D、12cm

查看试题解析
3. 如图，直线 $A B ∥ D C$ ， $∠ A = 40 °$ ， $∠ D = 45 °$ ，则 $∠ 1$ 的度数是（）

A、 $80 °$ B、 $85 °$ C、 $90 °$ D、 $95 °$

查看试题解析
4. 如图， $△ A B C ≌ △ C D A$ ，且 $A B = C D$ ，则下列结论错误的是（）

A、 $∠ 1 = ∠ 2$ B、 $A D = C B$ C、 $∠ D = ∠ B$ D、 $A B = B C$

查看试题解析
5. 中国古代数学名著《孙子算经》中有这样一个问题，大意是：“有100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，则大马、小马各有多少匹？”若设大马、小马各有x匹、y匹，根据题意，可列方程组为（）

A、 ${\begin{array}{l} x + y = 100 \\ 3 x + y = 100 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ x + 3 y = 100 \end{array}$ C、 ${\begin{array}{l} x + y = 100 \\ \frac{1}{3} x + 3 y = 100 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$

查看试题解析
6. 母亲节，小明去花店为妈妈准备节日礼物.已知康乃馨每支2元，百合每支3元.小明将30元钱全部用于购买这两种花（两种花都买），小明的购买方案共有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
7. 在下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 已知等腰三角形的一个底角比顶角大 $30 °$ ，则它的顶角的度数为（）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
9. 一个正多边形，它的每一个内角都等于 $140 °$ ，则该正多边形是（）

A、正六边形 B、正七边形 C、正八边形 D、正九边形

查看试题解析
10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方，图（2）是一个未完成的幻方，则x与y的和是（）

A、12 B、11 C、10 D、9

查看试题解析

二、填空题（本大题包括5小题，每小题3分，共15分）

11. 将方程 $2 x - 3 y = 6$ 变形为用含x的代数式表示y的形式：.

查看试题解析
12. 已知方程组 ${\begin{cases} x + y = m \\ x - y = n + 1 \end{cases}$ 的解是 ${\begin{cases} x = 3 \\ y = 2 \end{cases}$ ，则 $m + n$ 的值为.

查看试题解析
13. 关于x的方程 $x - a = 1 - 2 x$ 的解是一个非负数，则a的取值范围是.

查看试题解析
14. 如图，A、B、C分别是线段 $A_{1} B$ 、 $B_{1} C$ 、 $C_{1} A$ 的中点，若 $△ A B C$ 的面积是1，那么 $△ A_{1} B_{1} C_{1}$ 的面积为.

查看试题解析
15. 如图，四边形ABCD中， $∠ A = 100 °$ ， $∠ C = 70 °$ ，点M、N分别在AB、BC上，将 $△ B M N$ 沿MN翻折得到 $△ F M N$ .若 $M F ∥ A D$ ， $F N ∥ D C$ ，则 $∠ B$ 的度数为.

查看试题解析

三、填空题（本大题包括8小题，共75分）

16. 解方程：

(1)、 $\frac{1}{2} x - 3 = 2 x + \frac{1}{2}$

(2)、 $\frac{x - 3}{2} - \frac{2 x + 1}{3} = 1$

查看试题解析
17. 解方程组：

(1)、 ${\begin{array}{l} x - y = 1 \\ 3 x + y = 11 \end{array}$

(2)、 ${\begin{array}{l} 3 x - 2 y = 5 \\ 2 x + 3 y = 12 \end{array}$

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x + 1 < 3 x + 3 \\ \frac{2}{3} (x - 1) \leq \frac{1}{2} (x + \frac{1}{3}) \end{array}$ ，把解集在数轴上表示出来，并写出它的非负整数解.

查看试题解析
19. 如图，在 $△ A B C$ 中，D是AB上一点，E是AC上一点，BE、CD相交于点F， $∠ A = 62 °$ ， $∠ A C D = 35 °$ ， $∠ A B E = 20 °$ .求 $∠ B F D$ 的度数.

查看试题解析
20. 如图的方格纸中，每个小方格都是边长为1个单位长度的正方形，①②③均为顶点都在格点上的三角形（每个小方格的顶点叫做格点）.

(1)、图中，①经过一次变换（填“平移”“轴对称”或“旋转”）可以得到②；

(2)、图中，③是由①经过一次旋转变换得到的，其旋转中心是（填“A”“B”“C”或“D”）；

(3)、在图中画出①关于直线l成轴对称的图形④.

查看试题解析
21. 如图， $△ A B C$ 绕顶点A逆时针转 $30 °$ 至 $△ A D E$ ， $∠ B = 40 °$ ， $∠ D A C = 50 °$ .求 $∠ E$ 的度数.

查看试题解析
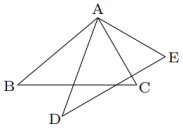22. 某中学计划为绘画兴趣小组购买A、B两种型号的颜料.若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元；若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.

(1)、求每盒A种型号的颜料和B种型号的颜料各多少元？

(2)、该中学决定购买以上两种型号共200盒，总费用不超过3920元，那么该中学最多可以购买多少盒A种型号的颜料？

查看试题解析
23. 问题情境：
如图1， $△ A B C$ 中，BO平分 $∠ A B C$ ， CO平分 $∠ A C D$ .

(1)、探索发现：
若 $∠ A = 60 °$ ，则 $∠ O$ 的度数为；若 $∠ A = 130 °$ ，则 $∠ O$ 的度数为.

(2)、猜想证明：
试判断 $∠ A$ 与 $∠ O$ 的关系，并说明理由.

(3)、结论应用：
如图2，在四边形MNCB中，BD平分 $∠ M B C$ ，且与四边形MNCB的外角 $∠ N C E$ 的平分线CD交于点D.若 $∠ B M N = 130 °$ ， $∠ C N M = 100 °$ ，则 $∠ D$ 的度数为.

查看试题解析