河南省驻马店市驿城区2022-2023学年七年级下册数学期末考试试卷
试卷更新日期:2023-07-07 类型:期末考试
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 随着微电子制造技术的不断进步,电子元件的尺寸大幅度减小.在芯片上的某种电子元件大约只占 , 将0.00000065用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若三角形的两边长分别为和 , 则下列长度的线段能作为第三边的是( )A、 B、 C、 D、5. 如图,直线 , 直线分别与直线、交于点、 , 点在直线上,.若 , 则的度数是( )
2. 随着微电子制造技术的不断进步,电子元件的尺寸大幅度减小.在芯片上的某种电子元件大约只占 , 将0.00000065用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若三角形的两边长分别为和 , 则下列长度的线段能作为第三边的是( )A、 B、 C、 D、5. 如图,直线 , 直线分别与直线、交于点、 , 点在直线上,.若 , 则的度数是( ) A、 B、 C、 D、6. 如图,点在一条直线上,已知 , , 下列条件中,不能判断的是( )
A、 B、 C、 D、6. 如图,点在一条直线上,已知 , , 下列条件中,不能判断的是( ) A、 B、 C、 D、7. 如图,边长为的大正方形中有一个边长为的小正方形,小颖将阴影部分的面积用两种不同的方法表示,能验证的等式是( )
A、 B、 C、 D、7. 如图,边长为的大正方形中有一个边长为的小正方形,小颖将阴影部分的面积用两种不同的方法表示,能验证的等式是( )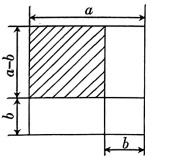 A、 B、 C、 D、8. 下面说法正确的是( )A、某彩票的中奖概率是 , 买20张彩票一定会有1张中奖 B、小明做了5次掷图钉的试验,其中3次钉尖朝上,则钉尖朝上的概率是 C、掷一枚质地均匀的硬币,前2次都是正面朝上,小亮认为第3次正面朝上的概率是 D、400人中有两人的生日在同一天是不可能事件9. 在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度与所挂物体的质量之间有如下关系:
A、 B、 C、 D、8. 下面说法正确的是( )A、某彩票的中奖概率是 , 买20张彩票一定会有1张中奖 B、小明做了5次掷图钉的试验,其中3次钉尖朝上,则钉尖朝上的概率是 C、掷一枚质地均匀的硬币,前2次都是正面朝上,小亮认为第3次正面朝上的概率是 D、400人中有两人的生日在同一天是不可能事件9. 在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度与所挂物体的质量之间有如下关系:0
1
2
3
4
5
…
10
10.5
11
11.5
12
12.5
…
在弹性限度内,所挂物体的质量为时,弹簧的长度为( )
A、 B、 C、 D、10. 如图,在等腰中, , 是边上的高,点是高上任意一点,点是边上任意一点, , , , 则的最小值是( ) A、3 B、5 C、 D、
A、3 B、5 C、 D、二、填空题(每小题3分,共15分)
-
11. 已知 , 则的值为 .12. 已知圆柱的底面半径是 , 圆柱的体积随着高的变化而变化,那么与之间的关系式为.13. 如图,一个转盘被分成6个相同的扇形,分别标有数字1,2,3,4,5,6,自由转动转盘,当转盘停止时,指针指向的数字大于4的概率是.
 14. 如图,一张三角形纸片中, , 点在边上,先将纸片沿折叠,点落在点处,交于点(如图1),再将沿折叠,点恰好落在折痕上的点处,此时(如图2),则的度数是.
14. 如图,一张三角形纸片中, , 点在边上,先将纸片沿折叠,点落在点处,交于点(如图1),再将沿折叠,点恰好落在折痕上的点处,此时(如图2),则的度数是. 15. 如图,在长方形中, , , 点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动,规定其中一个动点停止运动时,另一个动点也随之停止运动.当点的运动速度是时,与全等.
15. 如图,在长方形中, , , 点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动,规定其中一个动点停止运动时,另一个动点也随之停止运动.当点的运动速度是时,与全等.
三、解答题(本大题共8个小题,共75分)
-
16.(1)、计算:;(2)、化简:.17. 如图,已知 , .
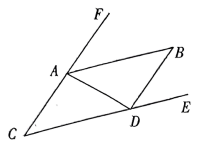 (1)、判断与所在直线是否平行,并说明理由;(2)、如果平分 , 且 , 求的度数.18. 如图,在中,平分 , 平分 , 于点.
(1)、判断与所在直线是否平行,并说明理由;(2)、如果平分 , 且 , 求的度数.18. 如图,在中,平分 , 平分 , 于点. (1)、若 , , 求的度数;(2)、若 , , 求的面积.19. 现有若干个除颜色外完全相同的球,从中选取10个球放入一个不透明的袋子里进行摸球游戏.(1)、若袋子中装有5个红球、2个白球和3个黄球,从中任意摸出一个球,摸到红球的概率是;(2)、小明和小亮一起做游戏,若袋子中有4个红球和6个白球,从中任意摸出一个球,摸到红球小明获胜,摸到白球小亮获胜,这个游戏对双方公平吗?说明理由;(3)、小颖在(2)中的袋子里随机摸出一个球,发现是白球,如果这个白球不放回,再从袋子里任意摸出一个球,摸到白球的概率是20. 学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题:
(1)、若 , , 求的度数;(2)、若 , , 求的面积.19. 现有若干个除颜色外完全相同的球,从中选取10个球放入一个不透明的袋子里进行摸球游戏.(1)、若袋子中装有5个红球、2个白球和3个黄球,从中任意摸出一个球,摸到红球的概率是;(2)、小明和小亮一起做游戏,若袋子中有4个红球和6个白球,从中任意摸出一个球,摸到红球小明获胜,摸到白球小亮获胜,这个游戏对双方公平吗?说明理由;(3)、小颖在(2)中的袋子里随机摸出一个球,发现是白球,如果这个白球不放回,再从袋子里任意摸出一个球,摸到白球的概率是20. 学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题: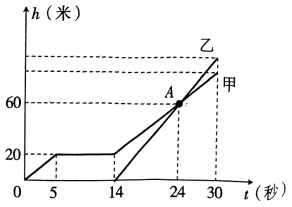 (1)、甲在空中停留时的高度是米,甲出发秒后乙开始起飞,点表示的意义是;(2)、甲、乙两架无人机的上升速度分别是多少米/秒?(3)、当时,两架无人机所在的高度相差多少米?21. 如图,线段是的中线,分别过点、作所在直线的垂线,垂足分别为、.
(1)、甲在空中停留时的高度是米,甲出发秒后乙开始起飞,点表示的意义是;(2)、甲、乙两架无人机的上升速度分别是多少米/秒?(3)、当时,两架无人机所在的高度相差多少米?21. 如图,线段是的中线,分别过点、作所在直线的垂线,垂足分别为、. (1)、请问与全等吗?说明理由;(2)、若的面积为10,的面积为6,求的面积.22. 如图,在中, , .
(1)、请问与全等吗?说明理由;(2)、若的面积为10,的面积为6,求的面积.22. 如图,在中, , .
尺规作图:
(1)、在线段上求作一点 , 使;②连接 , 以点为圆心,的长为半径画弧,交的延长线于点 , 连接.(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求的度数;(3)、在(1)的条件下,若 , 求的周长.23. (1)、【自主探究】
(1)、【自主探究】如图1,在四边形中, , , 点、分别在边、上,且 , 若 , , , 请计算线段的长度.
小明同学的做法是延长至点 , 使得 , 连接 , 他发现根据条件可证明 , 得到 , , 又和同学讨论发现,利用可证明 , 就能解决问题.那么他的结论是:线段的长度为.
(2)、【灵活运用】如图2,在四边形中, , , 点、分别在边、上,且 , 若和都不是直角,但满足 , 请猜想线段、、之间的数量关系:;
(3)、【拓,展延伸】如图3,在四边形中, , , 点、分别在边、上,且 , , 请问(2)中线段、、之间的数量关系是否仍然成立,并说明理由.