浙江省衢州市2022-2023学年高二下学期数学期末试题

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 若集合 $A = {x | 2^{2 x - 3} > 4}$ ， $B = {x | x \leq 5}$ ，则 $A ∩ B =$ （）

A、 ${x | x \leq \frac{5}{2}}$ B、 ${x | \frac{5}{2} < x \leq 5}$ C、 ${x | x < \frac{5}{2}}$ D、 ${x | x \leq 5}$

查看试题解析
2. 设 $z = \frac{1 + 3 i}{1 + i}$ （其中 $i$ 为虚数单位），则在复平面内 $z$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知直线 $m$ ， $n$ 和平面 $α$ ， $β$ ，则使平面 $α ⊥$ 平面 $β$ 成立的充分条件是（）

A、 $m ⊥ β$ ， $m ∥ α$ B、 $m ∥ β$ ， $n ∥ α$ C、 $α ∩ β = m$ ， $m ⊥ n$ ， $n \subset β$ D、 $m ⊥ β$ ， $m ⊥ α$

查看试题解析
4. 已知 $s i n (\frac{α}{2} + \frac{π}{4}) = \frac{\sqrt{6}}{3}$ ，则 $s i n α =$ （）

A、 $- \frac{1}{3}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
5. 函数 $y = l o g_{0.5} | x^{2} - x - 2 |$ 的单调递增区间为（）

A、 $(- \infty ， - 1)$ B、 $(2 ， + ∞)$ C、 $(- \infty ， - 1)$ 和 $(\frac{1}{2} ， 2)$ D、 $(- 1 ， \frac{1}{2})$ 和 $(2 ， + ∞)$

查看试题解析
6. 已知等差数列 ${a_{n}}$ 的前项和为 $S_{n}$ ，且 $S_{11} > S_{10} > S_{12}$ ，若 $b_{n} = 202 3^{a_{n}}$ ，数列 ${b_{n}}$ 的前 $n$ 项积为 $T_{n}$ ，则使 $T_{n} > 1$ 的最大整数 $n$ 为（）

A、20 B、21 C、22 D、23

查看试题解析
7. 已知函数 $f (x)$ 定义域为 $R$ ，对 $\forall x ， y \in R$ ，恒有 $f (x + y) + f (x - y) = 2 f (x) f (y)$ ，则下列说法错误的有（）

A、 $f (0) = 1$ B、 $f (2 x + 1) = f (- 2 x - 1)$ C、 $f (x) + f (0) \geq 0$ D、若 $f (1) = \frac{1}{2}$ ，则 $f (x)$ 周期为 $6$

查看试题解析
8. 衣柜里有5副不同颜色的手套，从中随机选4只，在取出两只是同一副的条件下，取出另外两只不是同一副的概率为（）

A、 $\frac{6}{7}$ B、 $\frac{12}{13}$ C、 $\frac{4}{7}$ D、 $\frac{13}{21}$

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 给出下列命题，其中正确的命题为（）

A、若样本数据 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{10}$ 的期望为3、方差为6，则数据 $2 x_{1} - 1 ， 2 x_{2} - 1 ， \cdot \cdot \cdot ， 2 x_{10} - 1$ 的期望为5、方差为11 B、假设经验回归方程为 $\hat{y} = 0.6 - 0.25 x$ ，则当 $x = 4$ 时， $y$ 的预测值为 $- 0.4$ C、随机变量 $X$ 服从正态分布 $N (2 ， σ^{2})$ ，若 $P (X > 4) = a$ ，则 $P (X < 0) = a$ D、甲同学所在的某校高三共有5000人，按简单随机抽样的方法抽取容量为200的一个样本.则甲被抽到的概率为 $\frac{1}{25}$

查看试题解析
10. 已知椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左，右焦点分别为 $F_{1}$ ， $F_{2}$ ，长轴长为4，点 $P (\sqrt{2} ， 1)$ 在椭圆 $Γ$ 外，点 $Q$ 在椭圆 $Γ$ 上，则（）

A、当椭圆 $Γ$ 的离心率的取值范围是 $(\frac{\sqrt{2}}{2} ， 1)$ B、当椭圆 $Γ$ 的离心率为 $\frac{\sqrt{3}}{2}$ 时， $| Q F_{1} |$ 的取值范围是 $[2 - \sqrt{3} ， 2 + \sqrt{3}]$ C、对任意点 $Q$ 都有 ${\vec{Q F}}_{1} \cdot \vec{Q F_{2}} > 0$ D、 $\frac{1}{| Q F_{1} |} + \frac{1}{| Q F_{2} |}$ 的最小值为2

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} 4 - | 4 x - 8 | ， 1 \leq x \leq 3 \\ \frac{1}{2} f (\frac{x}{3}) ， x > 3 \end{array}$ ，则下列说法正确的是（）

A、若函数 $y = f (x) - k x + k$ 有四个零点，则实数 $k$ 的取值范围是 $(\frac{1}{17} ， \frac{2}{5})$ B、关于 $x$ 的方程 $f (x) - \frac{1}{4} = 0$ 有8个不同的解 C、对于实数 $x \in [2 ， + ∞)$ ，不等式 $x f (x) - 10 \leq 0$ 恒成立 D、当 $x \in [3 ， 9]$ 时，函数 $f (x)$ 的图像与 $x$ 轴围成图形的面积为6

查看试题解析
12. 如图，在四棱锥 $P - A B C D$ 中， $A B ∥ C D$ ， $A D = C D = 1$ ， $∠ B A D = 120 °$ ， $∠ A C B = 90 °$ ， $P A ⊥ A C$ ，平面 $P A C ⊥$ 平面 $P B C$ ，点 $E$ 在棱 $P C$ 上且 $P E = 3 E C$ ，点 $F$ 是 $△ P A D$ 所在平面内的动点，点 $G$ 是 $△ P B C$ 所在平面内的动点，且点 $G$ 到直线 $B C$ 的距离与到点 $E$ 的距离相等，则（）

A、 $P A ⊥$ 平面 $A B C D$ B、若二面角 $D - P C - A$ 的余弦值为 $\frac{\sqrt{5}}{5}$ ，则点 $A$ 到平面 $P B C$ 的距离为 $\frac{\sqrt{5}}{5}$ C、若 $E F = \frac{\sqrt{10}}{4}$ ，则动点 $F$ 的轨迹长度为 $\frac{\sqrt{13}}{4} π$ D、若 $P A = 1$ ，则 $A G$ 的最小值为 $\frac{\sqrt{3}}{2}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

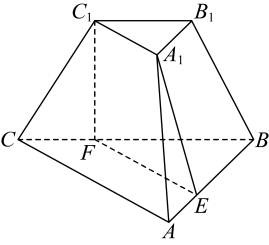
13. 在 ${(2 x - \frac{1}{x})}^{5}$ 的展开式中，各项系数的和是.

查看试题解析
14. 88键钢琴从左到右各键的音的频率组成一个递增的等比数列．若中音A（左起第49个键）的频率为 $440 H z$ ，钢琴上最低音的频率为 $27.5 H z$ ，则左起第61个键的音的频率为 $H z$ ．

查看试题解析
15. 设抛物线 $y^{2} = 4 x$ 的焦点为 $F$ ，准线为 $l$ ，过抛物线上一点 $P$ 作 $l$ 的垂线，垂足为 $Q$ ，若 $M (3 ， 0)$ ， $N (- 1 ， 0)$ ， $P F$ 与 $M Q$ 相交于点 $T$ ，且 $\vec{T N} + \vec{T P} = \vec{M T}$ ，则 $△ P T N$ 的面积为.

查看试题解析
16. 原有一块棱长为 $3 a$ 的正四面体石材，在搬运的过程有所损伤，剩下了一块所有棱长均为 $a$ 的八面体石材（如图），现将此八面体石材切削、打磨、加工成球，则加工后球的最大表面积与该八面体石材外接球的表面积之比为.

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 近期衢州市文化艺术中心进行了多次文艺演出，为了解观众对演出的喜爱程度，现随机调查了 $A$ 、 $B$ 两地区的200名观众，得到如下所示的2×2列联表.

非常喜欢
喜欢
合计
          $A$
60
30

          $B$
          $x$
          $y$

合计

若用分层抽样的方法在被调查的200名观众中随机抽取20名，则应从 $B$ 区且喜爱程度为“非常喜欢”的观众中抽取8名.
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
          $P (K^{2} \geq k_{0})$
0.05
0.010
0.001
          $k_{0}$
3.841
6.635
10.828

(1)、完成上述表格，并根据表格判断是否有95%的把握认为观众的喜爱程度与所在地区有关系.

(2)、若以抽样调查的频率为概率，从 $A$ 地区随机抽取3人，设抽到喜爱程度为“非常喜欢”的观众的人数为 $X$ ，求 $X$ 的数学期望.

查看试题解析
18. 已知数列 ${a_{n}}$ 满足： $a_{1} = a_{2} = 1$ ，对任意 $n \geq 3$ 且 $n \in N^{*}$ 时， $a_{n} = {\begin{array}{l} a_{n - 2} + n & n 是偶数， \\ 2 a_{[\frac{n}{3}]} & n 是奇数 . \end{array}$ 其中 $[x]$ 表示不超过 $x$ 的最大整数.

(1)、求 $a_{2 n}$ ；

(2)、设 $b_{n} = \frac{1}{a_{2 n} + 1} + a_{3^{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项 $S_{n}$ .

查看试题解析
19. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边为 $a$ ， $b$ ， $c$ ，已知 $t a n A = \frac{s i n B + s i n C}{c o s B + c o s C}$ .

(1)、求 $A$ ；

(2)、若 $c = 2$ ， $b - \frac{1}{2} c = \sqrt{6} c o s C$ ，求 $s i n C$ .

查看试题解析
20. 如图，在正三棱台 $A B C - A_{1} B_{1} C_{1}$ 中， $A_{1} B_{1} = 1$ ， $A B = 3$ ，过棱 $A_{1} C_{1}$ 的截面 $α$ 与棱 $A B$ ， $B C$ 分别交于 $E$ 、 $F$ .

(1)、记几何体 $E B F - A_{1} B_{1} C_{1}$ 和正三棱台 $A B C - A_{1} B_{1} C_{1}$ 体积分别为 $V_{1}$ ， $V_{2}$ ，若 $\frac{V_{1}}{V_{2}} = \frac{7}{13}$ ，求 $E F$ 的长度；

(2)、若 $B B_{1} = 2 \sqrt{3}$ ，求直线 $B B_{1}$ 与平面 $A C C_{1} A_{1}$ 所成角的正弦值.

查看试题解析
21. 已知函数 $f (x) = \frac{x}{e^{x}}$

(1)、若过点 $(0 ， m)$ 作函数 $f (x)$ 的切线有且仅有两条，求 $m$ 的值；

(2)、若对于任意 $k \in (- \infty ， 0)$ ，直线 $y = k x + b$ 与曲线 $y = f (x) (x \in (0 ， + \infty))$ 都有唯一交点，求实数 $b$ 的取值范围.

查看试题解析
22. 已知双曲线 $C ： x^{2} - \frac{y^{2}}{3} = 1$ ，过点 $P (2 ， \frac{9}{2})$ 作直线 $l$ 交双曲线 $C$ 的两支分别于 $A$ ， $B$ 两点，

(1)、若点 $P$ 恰为 $A B$ 的中点，求直线 $l$ 的斜率；

(2)、记双曲线 $C$ 的右焦点为 $F$ ，直线 $F A$ ， $F B$ 分别交双曲线 $C$ 于 $D$ ， $E$ 两点，求 $\frac{S_{△ F A B}}{S_{△ F D E}}$ 的取值范围.

查看试题解析

	非常喜欢	喜欢	合计
$A$	60	30
$B$	$x$	$y$
合计

$P (K^{2} \geq k_{0})$	0.05	0.010	0.001
$k_{0}$	3.841	6.635	10.828