浙江省杭州市2022-2023学年高二下学期数学期末试题

试卷更新日期：2023-07-07 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，有一项是符合题目要求的．

1. 直线 $3 x + 2 y - 1 = 0$ 的一个方向向量是（）

A、 $(2 ， - 3)$ B、 $(2 ， 3)$ C、 $(- 3 ， 2)$ D、 $(3 ， 2)$

查看试题解析
2. 若 ${\vec{a} ， \vec{b} ， \vec{c}}$ 是空间的一个基底，则也可以作为该空间基底的是（）

A、 $\vec{b} + \vec{c} ， \vec{b} ， - \vec{b} - \vec{c}$ B、 $\vec{a}$ ， $\vec{a} + \vec{b}$ ， $\vec{a} - \vec{b}$ C、 $\vec{a} + \vec{b}$ ， $\vec{a} - \vec{b}$ ， $\vec{c}$ D、 $\vec{a} + \vec{b} ， \vec{a} + \vec{b} + \vec{c} ， \vec{c}$

查看试题解析
3. “巴赫十二平均律”是世界上通用的音乐律制，它与五度相生律、纯律并称三大律制．“十二平均律”将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于 $\sqrt[12]{2}$ ．而早在16世纪，明代朱载最早用精湛的数学方法近似计算出这个比例，为这个理论的发展做出了重要贡献．若第一个单音的频率为 $f$ ，则第四个单音的频率为（）

A、 $5 f$ B、 $2^{\frac{1}{4}} f$ C、 $4 f$ D、 $2^{\frac{1}{3}} f$

查看试题解析
4. “点 $(a ， b)$ 在圆 $x^{2} + y^{2} = 1$ 外”是“直线 $a x + b y + 2 = 0$ 与圆 $x^{2} + y^{2} = 1$ 相交”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 第19届亚运会将于2023年9月23日在杭州开幕，因工作需要，还需招募少量志愿者．甲、乙等4人报名参加了“莲花”、“泳镜”、“玉琮”三个场馆的各一个项目的志愿者工作，每个项目仅需1名志愿者，每人至多参加一个项目．若甲不能参加“莲花”场馆的项目，则不同的选择方案共有（）

A、6种 B、12种 C、18种 D、24种

查看试题解析
6. $A$ ， $B$ 两个学科兴趣小组在实验室研究某粒子的运动轨迹，共同记录到粒子的一组坐标信息 $(x_{i} ， y_{i})$ ． $A$ 小组根据表中数据，直接对 $(x ， y)$ 作线性回归分析，得到：回归方程 $\hat{y} = 0.4699 x + 0.235$ ，决定系数 $R^{2} = 0.8732$ ． $B$ 小组先将数据按照变换 $u = x^{2}$ ， $v = y^{2}$ 进行整理，再对 $u$ ， $v$ 作线性回归分析，得到：回归方程 $\hat{v} = - 0.5006 u + 0.4922$ ，决定系数 $R^{2} = 0.9375$ ．根据统计学知识，下列方程中，最有可能是该粒子运动轨迹方程的是（）

A、 $0.4699 x - y + 0.235 = 0$ B、 $0.5006 x + y - 0.4922 = 0$ C、 $\frac{0.5006 x^{2}}{0.4922} + \frac{y^{2}}{0.4922} = 1$ D、 $\frac{x^{2}}{0.4922} + \frac{0.5006 y^{2}}{0.4922} = 1$

查看试题解析
7. 设 $A$ ， $B$ ， $C$ ， $D$ 是半径为1的球 $O$ 的球面上的四个点．设 $\vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$ ，则 $| A D | + | B D | + | C D |$ 不可能等于（）

A、3 B、 $\frac{7}{2}$ C、4 D、 $3 \sqrt{2}$

查看试题解析
8. 设椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点分别为 $F_{1}$ ， $F_{2}$ ， $P$ 是椭圆上不与顶点重合的一点，记 $I$ 为 $△ P F_{1} F_{2}$ 的内心．直线 $P I$ 交 $x$ 轴于 $A$ 点， $| \vec{O A} | = \frac{1}{4} c$ ，且 $\vec{P F_{1}} \cdot \vec{P F_{2}} = \frac{1}{16} a^{2}$ ，则椭圆 $C$ 的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 若函数 $f (x)$ 导函数的部分图像如图所示，则（）

A、 $x_{1}$ 是 $f (x)$ 的一个极大值点 B、 $x_{2}$ 是 $f (x)$ 的一个极小值点 C、 $x_{3}$ 是 $f (x)$ 的一个极大值点 D、 $x_{4}$ 是 $f (x)$ 的一个极小值点

查看试题解析
10. 抛掷一枚质地均匀的骰子（六个面上的数字是 $1$ 、 $2$ 、 $3$ 、 $4$ 、 $5$ 、 $6$ ），抛掷两次．设事件 $A ：$ “两次向上的点数之和大于 $7$ ”，事件 $B ：$ “两次向上的点数之积大于 $20$ ”，事件 $C ：$ “两次向上的点数之和小于 $10$ ”，则（）

A、事件 $B$ 与事件 $C$ 互斥 B、 $P (A B) = \frac{5}{72}$ C、 $P (B | A) = \frac{2}{5}$ D、事件 $A$ 与事件 $C$ 相互独立

查看试题解析
11. 设双曲线 $C ： \frac{x^{2}}{a} - \frac{y^{2}}{a^{2} - a + 4} = 1 (a > 0)$ ，直线 $l$ 与双曲线 $C$ 的右支交于点 $A$ ， $B$ ，则下列说法中正确的是（）

A、双曲线 $C$ 离心率的最小值为4 B、离心率最小时双曲线 $C$ 的渐近线方程为 $\sqrt{3} x \pm y = 0$ C、若直线 $l$ 同时与两条渐近线交于点 $C$ ， $D$ ，则 $| A C | = | B D |$ D、若 $a = 1$ ，点 $A$ 处的切线与两条渐近线交于点 $E$ ， $F$ ，则 $S_{△ E O F}$ 为定值

查看试题解析
12. 已知曲线 $f (x) = \frac{x}{e^{x}}$ ， $g (x) = \frac{l n x}{x}$ ，及直线 $y = a$ ，下列说法中正确的是（）

A、曲线 $f (x)$ 在 $x = 0$ 处的切线与曲线 $g (x)$ 在 $x = 1$ 处的切线平行 B、若直线 $y = a$ 与曲线 $f (x)$ 仅有一个公共点，则 $a = \frac{1}{e}$ C、曲线 $f (x)$ 与 $g (x)$ 有且仅有一个公共点 D、若直线 $y = a$ 与曲线 $f (x)$ 交于点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，与曲线 $g (x)$ 交于点 $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ ，则 $x_{1} x_{3} = x_{2}^{2}$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分．

13. $(x - y) (x + y)^{8}$ 的展开式中 $x^{3} y^{6}$ 的系数为．

查看试题解析
14. 曲率是衡量曲线弯曲程度的重要指标．定义：若 $f^{'} (x)$ 是 $f (x)$ 的导函数， $f^{″} (x)$ 是 $f^{'} (x)$ 的导函数，则曲线 $y = f (x)$ 在点 $(x ， f (x))$ 处的曲率 $K = \frac{| f^{″} (x) |}{{[1 + {(f^{'} (x))}^{2}]}^{\frac{3}{2}}}$ ．已知 $f (x) = c o s (x - 1) - l n x$ ，则曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的曲率为．

查看试题解析
15. 已知数列 ${a_{n}}$ 满足 $a_{2} = 8$ ， $a_{n} = [2^{{(- 1)}^{n}} + n] a_{n - 1} (n \geq 2 ， n \in N^{*})$ ，数列 ${b_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $b_{n} = l o g_{2} (a_{2 n + 2} \cdot a_{2 n - 1}) - l o g_{2} (a_{2 n} \cdot a_{2 n + 1})$ ，则满足 $S_{n} - 5 > 0$ 的正整数 $n$ 的最小值为．

查看试题解析
16. 设函数 $f (x) = 2^{| x + 2 |} + c o s (\frac{π}{2} x)$ ，则使得 $f (x + 1) > f (2 x)$ 成立的 $x$ 的取值范围是．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 如图，在四面体 $A B C D$ 中， $\vec{A E} = λ \vec{A B}$ ， $\vec{A H} = λ \vec{A D}$ ， $\vec{C F} = (1 - λ) \vec{C B}$ ， $\vec{C G} = (1 - λ) \vec{C D}$ ， $λ \in (0 ， 1)$ ．

(1)、求证： $E$ 、 $F$ 、 $G$ 、 $H$ 四点共面．

(2)、若 $λ = \frac{1}{3}$ ，设 $M$ 是 $E G$ 和 $F H$ 的交点， $O$ 是空间任意一点，用 $\vec{O A}$ 、 $\vec{O B}$ 、 $\vec{O C}$ 、 $\vec{O D}$ 表示 $\vec{O M}$ ．

查看试题解析
18. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{4} = 4 S_{2}$ ， $a_{2 n} = 2 a_{n} + 1 (n \in N^{*})$ .

(1)、求数列 ${a_{n}}$ 的通项公式.

(2)、若 ${a_{n}}$ 中的部分项 $a_{b_{n}}$ 组成的数列 ${a_{b_{n}} + 1}$ 是以 $a_{1} + 1$ 为首项，2为公比的等比数列，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，所有棱长均为 $2$ ， $∠ A_{1} A C = 6 0^{∘}$ ， $A_{1} B = \sqrt{6}$ ．

(1)、证明：平面 $A_{1} A C C_{1} ⊥$ 平面 $A B C$ ．

(2)、求平面 $B A_{1} B_{1}$ 与平面 $A_{1} B_{1} C_{1}$ 的夹角的正弦值．

查看试题解析

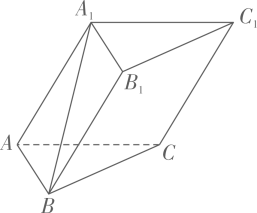20. 第19届亚运会将于2023年9月23日在杭州拉开帷幕，为了更好地迎接亚运会，杭州市政府大举加强了城市交通基础设施的建设．至2023年地铁运行的里程数达到516公里，排位全国第六．同时，一张总长464公里、“四纵五横”为骨架、通达“东西南北中”十城区的快速路网也顺利完工准备接待世界各地的来宾．现杭州公共出行的主流方式为地铁、公交、打车、共享单车这四种，基本可以覆盖大众的出行需求．

附： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ ．

$α$	0.050	0.010	0.001
$x_{α}$	3.841	6.635	10.828

(1)、一个兴趣小组发现，来自不同的城市的游客选择出行的习惯会有很大差异，为了验证这一猜想该小组进行了研究．请完成下列

2 \times 2

列联表，并根据小概率值

α = 0.010

的独立性检验，分析城市规模是否与出行偏好地铁有关？（精确到0.001）

单位：人

出行方式	国际大都市	中小型城市	合计
偏好地铁		20	100
偏好其他	60
合计		60

(2)、国际友人David来杭游玩，每日的行程分成

M (M \in N^{*})

段，为了更好的体验文化，相邻两段的出行方式不能相同，且选择地铁、公交、打车、共享单车的概率是等可能的．已知他每日从酒店出行的方式一定是从地铁开始，记第

n

段行程上David坐地铁的概率为

p_{n}

，易知

p_{1} = 1

，

p_{2} = 0

①试证明 ${p_{n} - \frac{1}{4}}$ 为等比数列；

②设第 $n$ 次David选择共享单车的概率为 $q_{n}$ ，比较 $p_{5}$ 与 $q_{5}$ 的大小．

查看试题解析

21. 设抛物线 $C ： y^{2} = 2 p y (p > 0)$ ，过焦点 $F$ 的直线与抛物线 $C$ 交于点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2}) .$ 当直线 $A B$ 垂直于 $x$ 轴时， $| A B | = 2$ ．

(1)、求抛物线 $C$ 的标准方程．

(2)、已知点 $P (1 ， 0)$ ，直线 $A P$ ， $B P$ 分别与抛物线 $C$ 交于点 $C$ ， $D$ ．
①求证：直线 $C D$ 过定点 $；$

②求 $△ P A B$ 与 $△ P C D$ 面积之和的最小值．

查看试题解析
22. 设函数 $f (x) = (x - 1)^{2} e^{x} - a x$ ，若曲线 $f (x)$ 在 $x = 0$ 处的切线方程为 $y = - 2 x + b$ ．

(1)、求实数 $a ， b$ 的值．

(2)、证明：函数 $f (x)$ 有两个零点．

(3)、记 $f^{'} (x)$ 是函数 $f (x)$ 的导数， $x_{1}$ ， $x_{2}$ 为 $f (x)$ 的两个零点，证明： $f^{'} (\frac{x_{1} + x_{2}}{2}) > - a$ ．

查看试题解析