江苏省徐州市2023年中考数学试卷
试卷更新日期:2023-07-07 类型:中考真卷
一、选择题(本大题共有8小题,在每小题所给出的四个选项中,只有一项符合题意,请将正确选项前的字母代号填涂答题卡相应位置)
-
1. 下列事件中的必然事件是( )A、地球绕着太阳转 B、射击运动员射击一次,命中靶心 C、天空出现三个太阳 D、经过有交通信号灯的路口,遇到红灯2. 下列图案是中心对称图形但不是轴对称图形的是( )A、
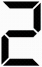 B、
B、 C、
C、 D、
D、 3. 如图,数轴上点分别对应实数 , 下列各式的值最小的是( )
3. 如图,数轴上点分别对应实数 , 下列各式的值最小的是( ) A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 徐州云龙山共九节,蜿蜒起伏,形似游龙,每节山的海拔如图所示.
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 徐州云龙山共九节,蜿蜒起伏,形似游龙,每节山的海拔如图所示.
其中,海拔为中位数的是( )
A、第五节山 B、第六节山 C、第八节山 D、第九节山6. 的值介于( )A、25与30之间 B、30与35之间 C、35与40之间 D、40与45之间7. 在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )A、 B、 C、 D、8. 如图,在中,为的中点.若点在边上,且 , 则的长为( )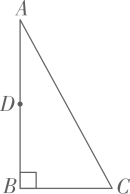 A、1 B、2 C、1或 D、1或2
A、1 B、2 C、1或 D、1或2二、填空题(本大题共有10小题,不需要写出解答过程,请将答案直接填写在答题卡相应位置)
-
9. 若一个三角形的边长均为整数,且两边长分别为3和5,则第三边的长可以为(写出一个即可).10. “五一”假期我市共接待游客约4370000人次,将4370000用科学记数法表示为 .11. 若代数式有意义,则x的取值范围是 .12. 正五边形的一个外角的大小为度.13. 关于x的方程有两个相等的实数根,则m的值是.14. 如图,在中,若 , 则°.
 15. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.
15. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.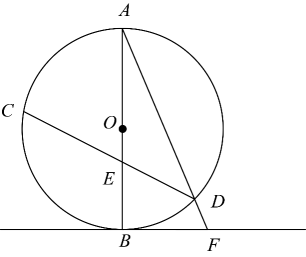 16. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角 , 则该圆锥的底面圆的半径r长为 .
16. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角 , 则该圆锥的底面圆的半径r长为 . 17. 如图,点在反比例函数的图象上,轴于点轴于点 . 一次函数与交于点 , 若为的中点,则的值为 .
17. 如图,点在反比例函数的图象上,轴于点轴于点 . 一次函数与交于点 , 若为的中点,则的值为 . 18. 如图,在中, , 点在边上.将沿折叠,使点落在点处,连接 , 则的最小值为 .
18. 如图,在中, , 点在边上.将沿折叠,使点落在点处,连接 , 则的最小值为 .
三、解答题(本大题共有10小题,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
-
19. 计算:(1)、;(2)、 .20.(1)、解方程组(2)、解不等式组21. 为了解某地区九年级学生的视力情况,从该地区九年级学生中抽查了部分学生,根据调查结果,绘制了如下两幅不完整的统计图.
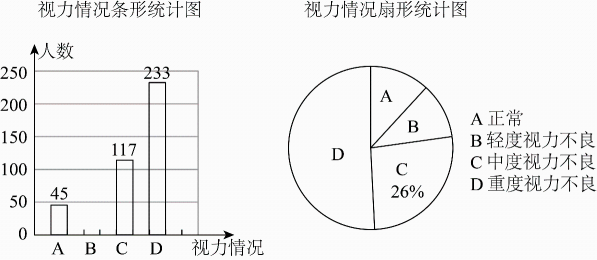
根据以上信息,解决下列问题:
(1)、此次调查的样本容量为;(2)、扇形统计图中对应圆心角度数为°;(3)、请补全条形统计图;(4)、若该地区九年级学生共有人,请估计其中视力正常的人数.22. 甲,乙、丙三人到淮海战役烈士纪念塔园林游览,若每人分别从纪念塔、纪念馆这两个景点中选择一个参观,且选择每个景点 机会相等,则三人选择相同景点的概率为多少? 23. 随着2022年底城东快速路的全线通车,徐州主城区与东区之间的交通得以有效改善,如图某人乘车从徐州东站至戏马台景区,可沿甲路线或乙路线前往.已知甲、乙两条路线的长度均为 , 甲路线的平均速度为乙路线的倍,甲路线的行驶时间比乙路线少 , 求甲路线的行驶时间.
机会相等,则三人选择相同景点的概率为多少? 23. 随着2022年底城东快速路的全线通车,徐州主城区与东区之间的交通得以有效改善,如图某人乘车从徐州东站至戏马台景区,可沿甲路线或乙路线前往.已知甲、乙两条路线的长度均为 , 甲路线的平均速度为乙路线的倍,甲路线的行驶时间比乙路线少 , 求甲路线的行驶时间. 24. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .
24. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .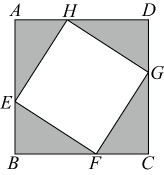 (1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.25. 徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点处,用测角仪测得塔顶的仰角 , 他在平地上沿正对电视塔的方向后退至点处,测得塔顶的仰角 . 若测角仪距地面的高度 , 求电视塔的高度(精确到 . (参考数据:)
(1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.25. 徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点处,用测角仪测得塔顶的仰角 , 他在平地上沿正对电视塔的方向后退至点处,测得塔顶的仰角 . 若测角仪距地面的高度 , 求电视塔的高度(精确到 . (参考数据:)
 26. 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.
26. 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系. (1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).
(1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
27. 【阅读理解】如图1,在矩形中,若 , 由勾股定理,得 , 同理 , 故 .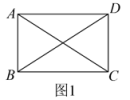 (1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由.
(1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由. (2)、【拓展提升】如图3,已知为的一条中线, . 求证: .
(2)、【拓展提升】如图3,已知为的一条中线, . 求证: . (3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 .
(3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 . 28. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .
28. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .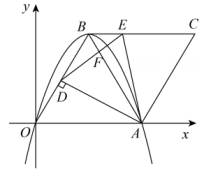 (1)、求点的坐标;(2)、随着点线段上运动.
(1)、求点的坐标;(2)、随着点线段上运动.①的大小是否发生变化?请说明理由;
②线段的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
(3)、当线段的中点在该二次函数的因象的对称轴上时,的面积为.