（冀教版）2023-2024学年七年级数学上册1.2 数轴期中复习

试卷更新日期：2023-07-07 类型：复习试卷

进入出卷网下载

一、选择题

1. 在数轴上，把表示 $- 2$ 的点沿着数轴移动7个单位长度得到的点所表示的数是（）

A、5 B、 $- 9$ C、 $\pm 5$ D、5或 $- 9$

查看试题解析
2. 在数轴上与表示数-3的点的距离等于2的点表示的数是（）

A、1 B、-5 C、-1或-5 D、-1或5

查看试题解析
3. 如图，数轴的单位长度为1，若点 $A$ 和点 $C$ 所表示的两个数的绝对值相等，则点 $B$ 表示的数是（）

A、－3 B、－1 C、1 D、3

查看试题解析
4. 如图，数轴的单位长度为1，数轴上有A，B，C三个点．若点A，B到原点的距离相等，则点C表示的数是（）

A、2 B、1 C、−1 D、−2

查看试题解析
5. 如图，数轴上点 $P$ 表示的有理数可能是（）

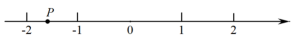A、-1.6 B、2.4 C、-0.6 D、-0.4

查看试题解析
6. 数轴上的点B到原点的距离是6，则点B表示的是为（）

A、12或 $- 12$ B、6 C、 $- 6$ D、6或 $- 6$

查看试题解析
7. 如下图，数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位度到达点C，若点C表示的数为1，则点A表示的数为（）

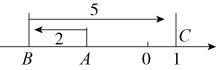A、-1 B、+1 C、-2 D、-3

查看试题解析
8. 已知a，b是有理数，若a在数轴上的对应点的位置如图所示， $a + b < 0$ ，有以下结论：① $b < 0$ ；② $b - a > 0$ ；③ $| - a | > - b$ ；④ $\frac{b}{a} < - 1$ ，则所有正确的结论是（）

A、①④ B、①③ C、②③ D、②④

查看试题解析
9. 小明在写作业时不慎将两滴墨水滴在数轴上，如图所示，此时墨迹盖住的整数共有（）个．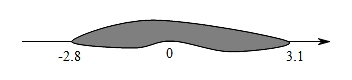

A、3 B、4 C、5 D、6

查看试题解析
10. 如图，数轴的单位长度为1．若点B和点C所表示的两个数的绝对值相等，则点A，D表示的数分别是（）

A、 $- 4$ ， 1 B、 $- 2$ ， 3 C、 $- 3$ ， 2 D、 $- 1$ ， 4

查看试题解析

二、填空题

11. 点 $A$ 为数轴上表示 $- 1$ 的点，若将点 $A$ 沿数轴一次平移一个单位，平移两次后到达点 $B$ ，则点 $B$ 表示的数是.

查看试题解析
12. 如图，已知数轴上的点 $C$ 表示的数为6，点 $A$ 表示的数为 $- 4$ ，点 $B$ 是 $A C$ 的中点，动点 $P$ 从点 $A$ 出发，以每秒2个单位长度的速度沿数轴向右匀速运动，运动时间为 $t$ 秒（ $t > 0$ ），另一动点 $Q$ ，从 $B$ 出发，以每秒1个单位长度的速度沿数轴向左匀速运动，且 $P$ ， $Q$ 同时出发，当 $t$ 为秒时，点 $P$ 与点 $Q$ 之间的距离为2个单位长度.

查看试题解析
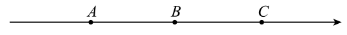13. 如图，图中数轴的单位长度为1，点A，B所表示的数互为相反数，若点M为线段 $C D$ 中点，则点M所表示的数为.

查看试题解析
14. 点A、B、P是数轴上不重合的三个点，点A表示的数为 $- 3$ ，点B表示的数为1，若A、B、P三个点中，其中一点到另外两点的距离相等时，我们称这三个点为“和谐三点”，则符合“和谐三点”的点P表示的数为.

查看试题解析
15. 数轴上的点M对应的数是-2，那么将点M向右移动4个单位长度，此时点M表示的数是。

查看试题解析

三、解答题

16. 把下面的直线补成条数轴，并在数轴上表示下列各数：﹣3， $\frac{1}{2}$ ， 0， $- \frac{3}{2}$ ， 2．

查看试题解析
17. 如图，在一条不完整的数轴上从左到右有点 $A ， B ， C$ ．其中 $A B = 2 ， B C = 1$ ．设点 $A ， B ， C$ 三点所表示的数的和为P，若以点B为原点，写出 $A ， C$ 两点所表示的数并计算出P的值．

查看试题解析
18. 在下面带有箭头的直线上先确定好原点以及单位长度，然后在所得的数轴上把下列各数表示出来：
﹣2，3.5，﹣1 $\frac{1}{2}$ ，2.75，2 $\frac{1}{3}$ ，﹣3．

查看试题解析
19. 已知A，B两点在数轴上表示的数分别是 $- 3$ 和12，现A，B两点分别以1个单位/秒，3个单位秒的速度向左运动，A比B早1秒出发，问B出发后几秒原点恰好在两点正中间？

查看试题解析

四、综合题

20. 如图，点A，B，C为数轴上三点，点A表示-2，点B表示4，点C表示8．

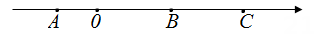(1)、A、C两点间的距离是.

(2)、当点P以每秒1个单位的速度从点C出发向CA方向运动时，是否存在某一时刻，使得PA=3PB？若存在，请求出运动时间；若不存在，请说明理由.

查看试题解析
21. 点O为数轴的原点，点A，B在数轴上的位置如图所示，点B表示的数为4，线段 $A B$ 的长为线段 $O B$ 长的1.5倍.点C在数轴上，M为线段 $O C$ 的中点.

(1)、点A表示的数为；

(2)、若线段 $B M = 5$ ，则线段 $O M$ 的长为；

(3)、若线段 $B C = a$ （ $0 < a < 4$ ），求线段 $A M$ 的长（用含a的式子表示）.

查看试题解析
22. 在数轴上有A、B两点，点B表示的数为b.对点A给出如下定义：当 $b \geq 0$ 时，将点A向右移动2个单位长度，得到点P；当 $b < 0$ 时，将点A向左移动 $| b |$ 个单位长度，得到点P.称点P为点A关于点B的“伴侣点”.如图，点A表示的数为 $- 1$ .

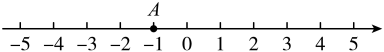(1)、在图中画出当 $b = 6$ 时，点A关于点B的“伴侣点”P；

(2)、当点P表示的数为-6，若点P为点A关于点B的“伴侣点”，则点B表示的数；

(3)、点A从数轴上表示-1的位置出发，以每秒1个单位的速度向右运动，点B从数轴上表示8的位置同时出发，以每秒2个单位的速度向左运动，两个点运动的时间为t秒.
①点B表示的数为（用含t的式子表示）；

②是否存在t，使得此时点A关于点B的“伴侣点”P恰好与原点重合？若存在，请求出t的值；若不存在，请说明理由.

查看试题解析
23. 同学们都知道，|4-(-2)|表示4与-2的差的绝对值，实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离；同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索：

(1)、|4-(-2)|=

(2)、若|x-2|=5，求x的值；

(3)、求|x-1|+|x+2|的最小值

查看试题解析

（冀教版）2023-2024学年七年级数学上册1.2 数轴 期中复习

一、选择题

二、填空题

三、解答题

四、综合题

（冀教版）2023-2024学年七年级数学上册1.2 数轴期中复习