（冀教版）2023-2024学年八年级数学上册13.1 命题与证明 期中复习
试卷更新日期：2023-07-06 类型：复习试卷
一、选择题
-
1. 下列说法正确的是（ ）A、每个定理都有逆定理 B、每个命题都有逆命题 C、假命题没有逆命题 D、真命题的逆命题是真命题2. 下列命题的逆命题是假命题的是（ ）A、直角三角形的两个锐角互余 B、两直线平行，内错角相等 C、三条边对应相等的两个三角形是全等三角形 D、若 ， 则3. 在下列各原命题中，逆命题是真命题的是（ ）A、直角三角形两个锐角互余 B、对顶角相等 C、全等三角形对应角相等 D、全等的两个三角形面积相等4. 下列命题的逆命题一定成立的有（ ）A、对顶角相等 B、若 ， 则 C、若 ， 则 D、同位角相等，两直线平行5. 关于原命题“如果 ， 那么”和它的逆命题“如果 ， 那么”，下列说法正确的是（ ）A、原命题是真命题，逆命题是假命题 B、原命题、逆命题都是真命题 C、原命题是假命题，逆命题是真命题 D、原命题，逆命题都是假命题6. 下列语句不是命题的是 （ ）A、x与y的和等于x+y吗？ B、不平行的两条直线只有一个交点 C、两点之间线段最短 D、相等的角是对顶角7. 下列句子是命题的是（ ）A、画 B、小于直角的角是锐角吗？ C、连结CD D、若 ， 则8. 下列命题：①全等三角形的对应角相等；②线段垂直平分线上的点到线段两端的距离相等；③等腰三角形的两个底角相等．其中逆命题是真命题的个数是（ ）A、0 B、1 C、2 D、39. 可以用来说明命题“若a＞b，则|a|＞|b|”是假命题的反例是（ ）A、a＝0，b＝-1 B、a＝1，b＝0 C、a＝2，b＝1 D、a＝2，b＝-110. 下列语句中是命题的有（ ）
①线段垂直平分线上的点到线段两端的距离相等；
②作点A关于直线l的对称点
③三边对应相等的两个三角形全等吗？
④角平分线上的点到角两边的距离相等.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 命题：直角三角形两条直角边的平方和等于斜边的平方，其逆命题是.12. 命题“全等三角形的面积相等”的逆命题是.（填“真命题”或“假命题”）13. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……，那么……”的形式为 ．14. “若 ， 则 ， ”命题（选填“是”或“不是”）．15. “如果 ， 那么”的逆命题是.
三、解答题
-
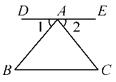
16. 下列各命题的条件是什么？结论是什么？(1)、两直线平行，同位角相等；(2)、过一点有且只有一条直线与已知直线平行．17. 如图所示，在①DE∥BC；②∠1＝∠2；③∠B＝∠C三个条件中，任选两个作题设，另一个作为结论，组成一个命题，并证明．
18. 指出下列命题的条件和结论，并改写成“如果…，那么…”的形式．
(1)、两直线平行，内错角相等；(2)、三角形内角和等于 180°．19. 下列各语句中个，哪些是命题，哪些不是命题？是命题的，请先将它改写为“如果…那么…”的形式，再指出命题的条件和结论．①同号两数的和一定不是负数；
②若x=2，则1﹣5x=0；
③延长线断AB至C，使B是AC的中点；
④互为倒数的两个数的积为1．
四、综合题
-
20. 求证：顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半．
(1)、根据题意补全下图，并根据题设和结论，结合图形，用符号语言补充写出“已知”和“求证”．已知：在锐角中， ， ▲ ；
求证： ▲ ．
(2)、证明：21. 探究问题：已知∠ABC ， 画一个角∠DEF ， 使DE∥AB ， EF∥BC ， 且DE交BC于点P ． ∠ABC与∠DEF有怎样的数量关系？
(1)、我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．①图1中∠ABC与∠DEF数量关系为；图2中∠ABC与∠DEF数量关系为；
请选择其中一种情况说明理由．
②由①得出一个真命题（用文字叙述）： ．
(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．
