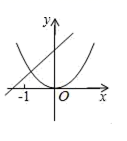2023-2024学年沪科版数学九年级上册21.2二次函数y=ax²图像性质【重难点梳理】

试卷更新日期：2023-07-06 类型：同步测试

进入出卷网下载

一、y=ax²开口方向及大小

1. 如图是四个二次函数的图象，则a、b、c、d的大小关系为（）

A、 $d < c < a < b$ B、 $d < c < b < a$ C、 $c < d < a < b$ D、 $c < d < b < a$

查看试题解析
2. 抛物线y= $\frac{1}{4}$ x² ， y=4x² ， y=－2x²的图像中，开口最大的是（）

A、y= $\frac{1}{4}$ x² B、y=4x² C、y=－2x² D、无法确定

查看试题解析

二、y=ax²的增减性

3. 二次函数 $y = x^{2}$ ，当 $- 1 \leq x \leq 3$ 时，函数值y的取值范围是（）

A、 $1 \leq y \leq 9$ B、 $0 \leq y \leq 9$ C、 $0 \leq y \leq 1$ D、 $y \geq 0$

查看试题解析
4. 已知点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 是函数 $y = (m - 3) x^{2}$ 图象上的两点，且当 $0 < x_{1} < x_{2}$ 时，有 $y_{1} < y_{2}$ ，则m的取值范围是（）

A、 $m > 3$ B、 $m \geq 3$ C、 $m < 3$ D、 $m \leq 3$

查看试题解析
5. 二次函数y= $(m + 2) x^{m^{2} - 3}$ ，当x<0时，y随x的增大而增大，则m= ．

查看试题解析

三、y=ax²的对称性

6. 在同一平面直角坐标系中作出 $y = 2 x^{2}$ ， $y = - 2 x^{2}$ ， $y = \frac{1}{2} x^{2}$ 的图象，它们的共同点是（）

A、关于y轴对称，抛物线的开口向上 B、关于y轴对称，抛物线的开口向下 C、关于y轴对称，抛物线的顶点都是原点 D、当 $x > 0$ 时，y随x的增大而减小

查看试题解析
7. 如图，正方形 $A B C D$ 、 $C E F G$ 的顶点D、F都在抛物线 $y = - \frac{1}{2} x^{2}$ 上，点B、C、E均在y轴上．若点O是 $B C$ 边的中点，则正方形 $C E F G$ 的边长为．

查看试题解析
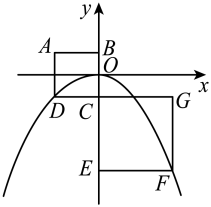8. 如图，在平面直角坐标系中，点A在抛物线 $y = x^{2}$ 上，过点A作y轴的垂线，交抛物线于另一点B．点C、D为线段AB的三等分点，分别过点C、D作x轴的垂线，交抛物线于点E、F，连接EF．若CE=16，则线段EF的长为．

查看试题解析
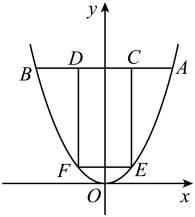9. 如图，在平面直角坐标系中，平行于x轴的直线，与二次函数y＝x²、y＝ax²分别交于A、B和C、D，若CD＝2AB，则a为（）

A、4 B、 $\frac{1}{4}$ C、2 D、 $\frac{1}{2}$

查看试题解析
10. 二次函数 $y = \sqrt{3} x^{2}$ 的图象如图，点 $A$ 在 $y$ 轴的正半轴上，点 $B$ ， $C$ 在二次函数 $y = \sqrt{3} x^{2}$ 的图象上，四边形 $O B A C$ 为菱形，且 $∠ A C O = 120 °$ ，则菱形 $O B A C$ 的面积为．

查看试题解析
11. 如图，⊙O的半径为2，C₁是函数y＝ $\frac{1}{2}$ x²的图象，C₂是函数y＝－ $\frac{1}{2}$ x²的图象，则阴影部分的面积是.

查看试题解析

四、二次项系数a的几何特性

12. 下列说法错误的是（）．

A、二次函数 $y = 3 x^{2}$ 中，当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 B、二次函数 $y = - 6 x^{2}$ 中，当 $x = 0$ 时， $y$ 有最大值 C、 $a$ 越大图象开口越小， $a$ 越小图象开口越大 D、不论 $a$ 是正数还是负数，抛物线 $y = a x^{2} (a \neq 0)$ 的顶点一定是坐标原点

查看试题解析
13. 在二次函数①y＝3x²；② $y = \frac{2}{3} x^{2} ； ③ y = \frac{4}{3} x^{2}$ 中，图象在同一水平线上的开口大小顺序用题号表示应该为（）

A、①＞②＞③ B、①＞③＞② C、②＞③＞① D、②＞①＞③

查看试题解析
14. 如图，正方形 $O A B C$ 的顶点B在抛物线 $y = 2 x^{2}$ 的第一象限的图象上，若点B的纵坐标是横坐标的2倍，则对角线 $A C$ 的长为.

查看试题解析
15. 如图，正方形 $O A B C$ 的顶点 $B$ 在抛物线 $y = x^{2}$ 的第一象限的图象上，若点 $B$ 的横坐标与纵坐标之和等于6，则对角线 $A C$ 的长为．

查看试题解析

五、y=ax²含参问题（取值范围）

16. 如图，在平面直角坐标系中有 $M (1 ， 2)$ ， $N (3 ， 3)$ 两点，如果抛物线 $y = a x^{2} (a > 0)$ 与线段 $M N$ 没有公共点，则a的取值范围是．

查看试题解析
17. 如图，在平面直角坐标系中，A（-2，-1），B（-1，-1），若抛物线 $y = a x^{2} (a \neq 0)$ 与线段AB有交点，则 $a$ 的取值范围是.

查看试题解析
18. 如图，正方形四个顶点的坐标依次为(1，1)，(3，1)，(3，3)，(1，3)，若抛物线y＝ax²的图象与正方形的边有公共点，则实数a的取值范围是．

查看试题解析

六、y=ax²函数图像共存问题

19. 已知a≠0，在同一平面直角坐标系中，函数y＝ax与y＝ax²的图象有可能是（）

A、 B、 C、 D、

查看试题解析
20. 二次函数 $y ＝ a x^{2}$ 与一次函数 $y ＝ a x + a$ 在同一坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析