广东省广州市花都区重点中学2022-2023学年高二下册期中考试数学试卷
试卷更新日期:2023-07-06 类型:期中考试
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
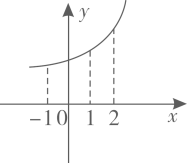
1. 从地到地要经过地,已知从地到地有三条路,从地到地有四条路,则从地到地不同的走法种数是( )A、 B、 C、 D、2. 已知函数的图象如图所示,设函数从到的平均变化率为 , 从到的平均变化率为 , 则与的大小关系为( )
 A、 B、 C、 D、不确定3. 若数列满足: , 且 , 则前项和为( )A、 B、 C、 D、4. 设函数的导函数为 , 若 , 则( )A、 B、 C、 D、5. 甲、乙、丙、丁、戊、己人站成一排拍合照,要求甲必须站在中间两个位置之一,且乙、丙人相邻,则不同的排队方法共有( )A、种 B、种 C、种 D、种6. 用种不同颜色给图中的、、、四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,共有种不同的涂色方案.( )
A、 B、 C、 D、不确定3. 若数列满足: , 且 , 则前项和为( )A、 B、 C、 D、4. 设函数的导函数为 , 若 , 则( )A、 B、 C、 D、5. 甲、乙、丙、丁、戊、己人站成一排拍合照,要求甲必须站在中间两个位置之一,且乙、丙人相邻,则不同的排队方法共有( )A、种 B、种 C、种 D、种6. 用种不同颜色给图中的、、、四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,共有种不同的涂色方案.( )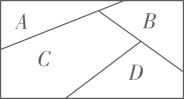 A、 B、 C、 D、7. 已知抛物线:的焦点为 , 抛物线上一点到点的距离为 , 则点到原点的距离为( )A、 B、 C、 D、8. 已知是定义在上的函数,其导函数为 , 且不等式恒成立,则下列不等式成立的是( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知抛物线:的焦点为 , 抛物线上一点到点的距离为 , 则点到原点的距离为( )A、 B、 C、 D、8. 已知是定义在上的函数,其导函数为 , 且不等式恒成立,则下列不等式成立的是( )A、 B、 C、 D、二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
9. 定义在上的可导函数的导函数的图象如图所示,以下结论正确的是( )
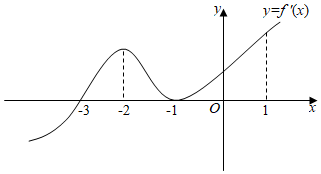 A、是的一个极小值点 B、和都是的极大值点 C、的单调递增区间是 D、的单调递减区间是10. 某学生想在物理、化学、生物、政治、历史、地理、技术这七门课程中选三门作为选考科目,下列说法正确的是( )A、若任意选择三门课程,则选法种数为 B、若物理和化学至少选一门,则选法种数为 C、若物理和历史不能同时选,则选法种数为 D、若物理和化学至少选一门,且物理和历史不能同时选,则选法种数为11. 在的展开式中,下列说法正确的是( )A、常数项是 B、第四项和第六项的系数相等 C、各项的二项式系数之和为 D、各项的系数之和为12. 已知函数 , 则( )A、的值域为 B、直线是曲线的一条切线 C、图象的对称中心为 D、方程有三个实数根
A、是的一个极小值点 B、和都是的极大值点 C、的单调递增区间是 D、的单调递减区间是10. 某学生想在物理、化学、生物、政治、历史、地理、技术这七门课程中选三门作为选考科目,下列说法正确的是( )A、若任意选择三门课程,则选法种数为 B、若物理和化学至少选一门,则选法种数为 C、若物理和历史不能同时选,则选法种数为 D、若物理和化学至少选一门,且物理和历史不能同时选,则选法种数为11. 在的展开式中,下列说法正确的是( )A、常数项是 B、第四项和第六项的系数相等 C、各项的二项式系数之和为 D、各项的系数之和为12. 已知函数 , 则( )A、的值域为 B、直线是曲线的一条切线 C、图象的对称中心为 D、方程有三个实数根三、填空题(本大题共4小题,共20.0分)
-
13. 曲线在处的切线方程为 .14. 900的正因数有个.(用数字作答)15. 写出与直线 , , 和圆都相切的一个圆的方程 .16. 展开式中含项的系数为 .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 在的展开式中,求:(1)、第4项的二项式系数;(2)、常数项.18. 已知等比数列的各项均为正数,其前项和为 , 且 , , 成等差数列, .(1)、求数列的通项公式;(2)、设 , 求数列的前项和 .19. 如图,在直三棱柱中, , , , , 为的中点.
 (1)、求点到平面的距离;(2)、求二面角的正弦值.20. 某服装厂主要从事服装加工生产,依据以往的数据分析,若加工产品订单的金额为万元,可获得的加工费为万元,其中 .(1)、若 , 为确保企业获得的加工费随加工产品订单的金额的增长而增长,则该企业加工产品订单的金额单位:万元应在什么范围内?(2)、若该企业加工产品订单的金额为万元时共需要的生产成本为万元,已知该企业加工生产能力为其中为产品订单的金额 , 试问在何范围时,该企业加工生产将不会出现亏损.
(1)、求点到平面的距离;(2)、求二面角的正弦值.20. 某服装厂主要从事服装加工生产,依据以往的数据分析,若加工产品订单的金额为万元,可获得的加工费为万元,其中 .(1)、若 , 为确保企业获得的加工费随加工产品订单的金额的增长而增长,则该企业加工产品订单的金额单位:万元应在什么范围内?(2)、若该企业加工产品订单的金额为万元时共需要的生产成本为万元,已知该企业加工生产能力为其中为产品订单的金额 , 试问在何范围时,该企业加工生产将不会出现亏损.