浙江省台州市八校联盟2022-2023学年高一下册期中考试数学试卷
试卷更新日期:2023-07-06 类型:期中考试
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
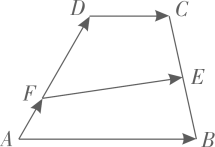
1. 已知复数是纯虚数,则实数( )A、 B、 C、 D、2. 如图,在中, , 若 , , 则( )
 A、 B、 C、 D、3. 已知空间中点 , , 直线 , 平面 , 若 , , , , 则下列结论正确的是( )A、 B、与相交 C、 D、以上都有可能4. 在中,角 , , 所对的边分别是 , , , 若 , , , 则( )A、 B、 C、 D、5. 如图,已知一个直四棱柱的侧棱长为 , 底面是对角线长分别是和的菱形,则这个四棱柱的侧面积是( )
A、 B、 C、 D、3. 已知空间中点 , , 直线 , 平面 , 若 , , , , 则下列结论正确的是( )A、 B、与相交 C、 D、以上都有可能4. 在中,角 , , 所对的边分别是 , , , 若 , , , 则( )A、 B、 C、 D、5. 如图,已知一个直四棱柱的侧棱长为 , 底面是对角线长分别是和的菱形,则这个四棱柱的侧面积是( ) A、 B、 C、 D、6. 在中,为边上的任意一点,点在线段上,且满足 , 若 , 则的值为( )A、 B、 C、 D、7. 如图,在圆中, , 点 , 在圆上, , 则的值为( )
A、 B、 C、 D、6. 在中,为边上的任意一点,点在线段上,且满足 , 若 , 则的值为( )A、 B、 C、 D、7. 如图,在圆中, , 点 , 在圆上, , 则的值为( ) A、 B、 C、 D、8. 已知四棱锥中,平面 , 四边形为正方形, , 平面过 , , 的中点,则下列关于平面截四棱锥所得的截面正确的为( )A、所得截面是正五边形 B、截面过棱的三等分点 C、所得截面面积为 D、截面不经过中点
A、 B、 C、 D、8. 已知四棱锥中,平面 , 四边形为正方形, , 平面过 , , 的中点,则下列关于平面截四棱锥所得的截面正确的为( )A、所得截面是正五边形 B、截面过棱的三等分点 C、所得截面面积为 D、截面不经过中点二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
9. 已知复数 , , 下列结论正确的有( )A、 B、若 , 则的最大值为 C、 D、在复平面内对应的点在第二象限10. 在中,角、、的对边分别为 , , , 若 , , 则使此三角形有两解的的值可以是( )A、5 B、 C、8 D、11. 的内角 , , 的对边分别为 , , , 其外接圆半径为 , 下列结论正确的有( )A、若 , , 则 B、若 , 则可能是直角三角形 C、若 , 则 D、若 , 则是直角三角形12. 如图,圆锥底面的直径为 , : , 为的中点,则下列说法正确的有( )
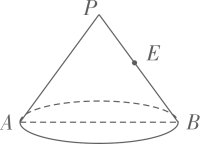 A、圆锥的体积为 B、圆锥内切球的半径为 C、过截圆锥所得截面面积最大为 D、点沿圆锥表面到的最短路经长为
A、圆锥的体积为 B、圆锥内切球的半径为 C、过截圆锥所得截面面积最大为 D、点沿圆锥表面到的最短路经长为三、填空题(本大题共4小题,共20.0分)
-
13. 已知向量 , , , 若 , 则 .14. 已知复数满足 , 则的取值范围为 .15. 已知圆柱体的底面半径为 , 高为 , 一只蜗牛从圆柱体底部开始爬行,绕圆柱体圈到达顶部,则蜗牛爬行的最短路径长为 .16. 在中, , , , 对任意 , 有恒成立,点是直线上,则的最小值是 .

四、解答题(本大题共5小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已如为虚数单位,复数 .(1)、当实数取何值时,是纯虚数;(2)、若 , 求的值.18. 已知在中,角 , , , 所对的边为 , , , 若 .(1)、求角的大小;(2)、若 , 求面积的最大值.19. 台州黄岩被誉为“模具之乡”,为市场对球形冰淇淋的需求,特地制作了一款中空的正三棱柱模具,其内壁恰好是球体的表面,且内壁与棱柱的每一个面都相切内壁厚度忽略不计 , 店家可以将不同口味的冰淇淋放入该模具中,再通过按压的方式得到球形冰淇淋已知该模具底部边长为 .

⑴求内壁的面积;
⑵求制作该模具所需材料的体积;
⑶求模具顶点到内壁的最短距离.