吉林省长春吉大附高2023年高三第五次模拟考试数学试卷
试卷更新日期:2023-07-06 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
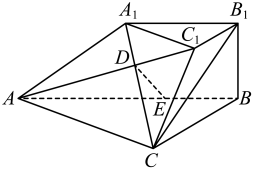
1. 已知(为虚数单位),则( )A、 B、 C、 D、2. 集合满足 , , 则集合中的元素个数为( )A、3 B、4 C、5 D、63. 庑殿(图1)是中国古代传统建筑中的一种屋顶形式,多用于宫殿、坛庙、重要门楼等高级建筑上,庑殿的基本结构包括四个坡面,坡面相交处形成5根屋脊,故又称“四阿殿”或“五脊殿”.图2是根据庑殿顶构造的多面体模型,底面是矩形,且四个侧面与底面的夹角均相等,则( ).

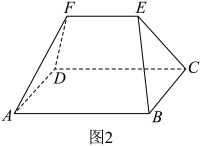 A、 B、 C、 D、4. 在数列中,若 , 则( )A、 B、 C、 D、5. 已知为异面直线,平面 , 平面 , 若直线满足 , 且.则下列说法正确的是( )A、 B、 C、与相交,且交线平行于 D、与相交,且交线垂直于6. 已知 , 若点为曲线:与曲线:的交点,且两条曲线在点处的切线重合,则实数的最大值为( )A、 B、 C、 D、7. 如图,在所在平面内,分别以为边向外作正方形和正方形 . 记的内角的对边分别为 , 面积为 , 已知 , 且 , 则( )
A、 B、 C、 D、4. 在数列中,若 , 则( )A、 B、 C、 D、5. 已知为异面直线,平面 , 平面 , 若直线满足 , 且.则下列说法正确的是( )A、 B、 C、与相交,且交线平行于 D、与相交,且交线垂直于6. 已知 , 若点为曲线:与曲线:的交点,且两条曲线在点处的切线重合,则实数的最大值为( )A、 B、 C、 D、7. 如图,在所在平面内,分别以为边向外作正方形和正方形 . 记的内角的对边分别为 , 面积为 , 已知 , 且 , 则( )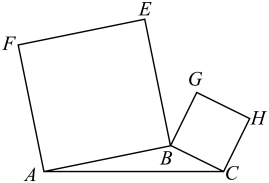 A、 B、 C、 D、
A、 B、 C、 D、二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
8. 已知展开式中的第三项的系数为45,则( )A、 B、展开式中所有系数和为 C、二项式系数最大的项为中间项 D、含的项是第7项9. 2022年11月17日,工业和信息化部成功举办第十七届“中国芯”集成电路产业大会.此次大会以“强芯固基以质为本”为主题,旨在培育壮大我国集成电路产业,夯实产业基础、营造良好产业生态.某芯片研发单位用在“A芯片”上研发费用占本单位总研发费用的百分比如表所示.已知 , 于是分别用p=和p=得到了两条回归直线方程: , , 对应的相关系数分别为、 , 百分比y对应的方差分别为、 , 则下列结论正确的是( )(附: , )
年份
年份代码x
p
q
A、 B、 C、 D、10. 设 , 圆(为圆心),为圆上任意一点,线段的中点为 , 过点作线段的垂线与直线相交于点 . 当点在圆上运动时,点的轨迹为曲线 , 点的轨迹为曲线 , 则下列说法正确的有( )A、曲线的方程为 B、当点在圆上时,点的横坐标为 C、曲线的方程为 D、与无公共点11. 若正实数满足 , 且 , 则下列不等式一定成立的是( )A、 B、 C、 D、三、填空题:本题共4小题,每小题5分,共20分.
-
12. 设 , 若 , 则a的取值范围为.13. 已知圆及直线 , 当直线被圆截得的弦长为时,的值等于.14. 已知正四棱柱的体积为 , 侧棱 , 是棱的中点,是侧棱上的动点,直线交平面于点 , 则动点的轨迹长度为 .15. 将数列中的项排成下表:
,
, , ,
, , , , , , ,
…
已知各行的第一个数 , , , , …构成数列 , 且的前项和满足(且),从第三行起,每一行中的数按从左到右的顺序均构成等差数列,且公差为同一个常数.若 , 则第6行的所有项的和为.
四、解答题:本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
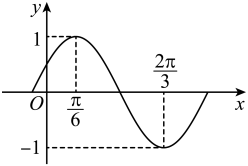
16. 已知函数( , , )的部分图象如图所示.
 (1)、求的解析式;(2)、设 , 若函数在区间上单调递增,求实数的最大值.17. 数列 , 满足 , , .(1)、求证:是常数列;(2)、设 , , 求的最大项.18. 甲、乙足球爱好者为了提高球技,两人轮流进行点球训练(每人各踢一次为一轮),在相同的条件下,每轮甲、乙两人在同一位置,一人踢球另一人扑球,甲先踢,每人踢一次球,两人有1人进球另一人不进球,进球者得1分,不进球者得分;两人都进球或都不进球,两人均得0分,设甲、乙每次踢球命中的概率均为 , 甲扑到乙踢出球的概率为 , 乙扑到甲踢出球的概率 , 且各次踢球互不影响.(1)、经过1轮踢球,记甲的得分为X,求X的分布列及数学期望;(2)、求经过3轮踢球累计得分后,甲得分高于乙得分的概率.
(1)、求的解析式;(2)、设 , 若函数在区间上单调递增,求实数的最大值.17. 数列 , 满足 , , .(1)、求证:是常数列;(2)、设 , , 求的最大项.18. 甲、乙足球爱好者为了提高球技,两人轮流进行点球训练(每人各踢一次为一轮),在相同的条件下,每轮甲、乙两人在同一位置,一人踢球另一人扑球,甲先踢,每人踢一次球,两人有1人进球另一人不进球,进球者得1分,不进球者得分;两人都进球或都不进球,两人均得0分,设甲、乙每次踢球命中的概率均为 , 甲扑到乙踢出球的概率为 , 乙扑到甲踢出球的概率 , 且各次踢球互不影响.(1)、经过1轮踢球,记甲的得分为X,求X的分布列及数学期望;(2)、求经过3轮踢球累计得分后,甲得分高于乙得分的概率.