浙江省湖州市2022-2023学年高一下册期末考试数学试卷

试卷更新日期：2023-07-06 类型：期末考试

进入出卷网下载

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设集合 $A = {x | - 1 < x < 2}$ ，集合 $B = {x | x^{2} - 4 x + 3 < 0}$ ，则 $A ∪ B =$ （）

A、 ${x | - 1 < x < 3}$ B、 ${x | - 1 < x < 1}$ C、 ${x | 1 < x < 2}$ D、 ${x | 2 < x < 3}$

查看试题解析
2. 已知角 $α$ 的终边过点 $(- 1 ， 2)$ ，则 $s i n α$ 等于（）

A、 $- \frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $- \frac{2 \sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
3. 已知i为虚数单位，复数z满足 $i^{2023} (2 + z) = 2 - i$ ，则 $\bar{z} =$ （）

A、 $- 1 + 2 i$ B、 $- 1 - 2 i$ C、 $1 + 2 i$ D、 $1 - 2 i$

查看试题解析
4. 在空间中，l，m是不重合的直线， $α$ ， $β$ 是不重合的平面，则下列说法正确的是（）

A、若 $l \subset α$ ， $m \subset β$ ， $α ∥ β$ ，则 $l ∥ m$ B、若 $l ∥ m$ ， $m \subset β$ ，则 $l ∥ β$ C、若 $α ⊥ β$ ， $α ∩ β = m$ ， $l ⊥ m$ ，则 $l ⊥ β$ D、若 $l ⊥ α$ ， $l ∥ m$ ， $α ∥ β$ ，则 $m ⊥ β$

查看试题解析
5. 阿基米德是伟大的古希腊数学家，他和高斯、牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），球的体积是圆柱体积的三分之二，球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型，其圆柱表面积为 $36 π$ ，则该模型中圆柱的体积与球的体积之和为（）

A、 $8 \sqrt{6} π$ B、 $12 \sqrt{6} π$ C、 $20 \sqrt{6} π$ D、 $48 \sqrt{6} π$

查看试题解析
6. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} \cdot \vec{b} = 5$ ，且 $\vec{b} = (3 ， - 4)$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为（）

A、 $(\frac{3}{5} ， - \frac{4}{5})$ B、 $(- \frac{3}{5} ， \frac{4}{5})$ C、 $(3 ， - 4)$ D、 $(- 3 ， 4)$

查看试题解析
7. “忽登最高塔，眼界穷大千.卞峰照城郭，震泽浮云天.”这是苏东坡笔下的湖城三绝之一“塔里塔”飞英塔.某学生为测量其高度，在远处选取了与该建筑物的底端B在同一水平面内的两个测量基点C与D，现测得 $∠ B C D = 45 °$ ， $∠ B D C = 105 °$ ， $C D = 18$ 米，在点C处测得飞英塔顶端A的仰角 $∠ A C B = 58 °$ ，则飞英塔的高度约是（）（参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{6} \approx 2.4$ ， $t a n 58 ° \approx 1.6$ ）

A、45米 B、50米 C、55米 D、60米

查看试题解析
8. 三棱锥 $P - A B C$ 中，平面 $P A B ⊥$ 平面ABC， $△ A B C$ 是边长为2的正三角形， $P A = P B = \sqrt{3}$ ，则三棱锥 $P - A B C$ 外接球的表面积为（）

A、 $\frac{35 π}{3}$ B、 $\frac{35 π}{6}$ C、 $\frac{35 π}{12}$ D、 $\frac{35 π}{24}$

查看试题解析

二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.

9. 某中学为了解大数据提供的个性化作业的质量情况，随机访问50名学生，根据这50名学生对个性化作业的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间 $[40 ， 50)$ ， $[50 ， 60)$ ， …， $[80 ， 90)$ ， $[90 ， 100]$ .（）

A、频率分布直方图中a的值为0.006 B、估计该中学学生对个性化作业的评分不低于80的概率为0.04 C、从评分在 $[40 ， 60)$ 的受访学生中，随机抽取2人，此2人评分都在 $[40 ， 50)$ 的概率为 $\frac{1}{10}$ D、受访学生对个性化作业评分的第40百分位数为72.6

查看试题解析
10. 先后两次掷一枚质地均匀的骰子，A表示事件“第一次掷出的点数是5”，B表示事件“第二次掷出的点数是偶数”，C表示事件“两次掷出的点数之和是5”，D表示事件“至少出现一个奇数点”，则（）

A、事件A与C互斥 B、 $P (D) = \frac{3}{4}$ C、事件B与D对立 D、事件B与C相互独立

查看试题解析
11. 设函数 $f (x) = s i n (2 x + \frac{π}{6}) + c o s (2 x - \frac{π}{3})$ ，则（）

A、函数 $f (x - \frac{π}{12})$ 是偶函数 B、函数 $f (x - \frac{π}{12})$ 是奇函数 C、函数 $f (x)$ 的图象可由函数 $y = 2 s i n 2 x$ 的图象向左平移 $\frac{π}{12}$ 个单位得到 D、函数 $y = | f (x) |$ 在区间 $[\frac{k π}{2} + \frac{π}{6} ， \frac{k π}{2} + \frac{5 π}{12}] (k \in Z)$ 上单调递增

查看试题解析
12. 已知正四棱台 $A B C D - E F G H$ 的所有顶点都在球O的球面上， $A E = \sqrt{2}$ ， $A B = 2 E F = 2$ ， M为△BDG内部（含边界）的动点，则（）

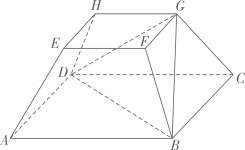A、直线AE与平面BDG相交 B、球O的体积为 $\frac{8 \sqrt{2}}{3} π$ C、直线AM与平面BDG所成角的最大值为 $\frac{π}{3}$ D、 $M A + M E$ 的取值范围为 $[2 \sqrt{2} ， 4]$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

13. 设向量 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 为单位正交基底，若 $\vec{a} = 2 \vec{e_{1}} - \vec{e_{2}}$ ， $\vec{b} = \vec{e_{1}} + k \vec{e_{2}}$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $k =$ .

查看试题解析
14. 已知采用分层抽样得到的高三男生、女生各100名学生的身高情况为：男生样本平均数为172cm，方差为120，女生样本平均数165cm，方差为120，则总体样本方差是.

查看试题解析
15. 在锐角三角形ABC中，已知 $2 s i n^{2} A + s i n^{2} B = 2 s i n^{2} C$ ，则 $\frac{t a n C}{t a n A} =$ ， $\frac{1}{t a n A} + \frac{1}{t a n B} + \frac{1}{t a n C}$ 的最小值是.

查看试题解析
16. 对任意的 $x \in [0 ， \frac{5}{2}]$ ，不等式 $\frac{t x - 1}{t^{2}} \leq e^{t^{2} - t x + 1}$ 恒成立，求正实数t的取值范围是.（其中 $e \approx 2.71828$ 是自然对数的底数）

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 习近平总书记指出：“要健全社会心理服务体系和疏导机制、危机干预机制，塑造自尊自信、理性平和、亲善友爱的社会心态.”在2022年新冠肺炎疫情防控阻击战中，心理医生的相关心理疏导起到了重要作用.某心理调查机构为了解市民在疫情期间的心理健康状况，随机抽取n位市民进行心理健康问卷调查，按所得评分（满分100分）从低到高将心理健康状况分为四个等级：

调查评分	$[40 ， 50)$	$[50 ， 60)$	$[60 ， 70)$	$[70 ， 80)$	$[80 ， 90)$	$[90 ， 100]$
心理等级	有隐患		一般		良好	优秀

并绘制如图所示的频率分布直方图.已知调查评分在 $[70 ， 80)$ 的市民为400人.

(1)、求n的值及频率分布直方图中t的值；

(2)、在抽取的心理等级为“有隐患”的市民中，按照调查评分分层抽取3人进行心理疏导.据以往数据统计，经过心理疏导后，调查评分在

[40 ， 50)

的市民心理等级转为“良好”的概率为

\frac{1}{4}

，调查评分在

[50 ， 60)

的市民心理等级转为“良好”的概率为

\frac{1}{3}

，若经过心理疏导后的恢复情况相互独立，试问在抽取的3人中，经过心理疏导后，至少有一人心理等级转为“良好”的概率为多少？

(3)、心理调查机构与该市管理部门设定的预案是：以抽取的样本作为参考，若市民心理健康指数平均值不低于0.8，则只需发放心理指导资料，否则需要举办心理健康大讲堂.根据你所学的统计知识，判断该市是否需要举办心理健康大讲堂，并说明理由.

注：每组数据以区间的中点值代替，心理健康指数＝问卷调查评分/100.

查看试题解析

18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A_{1} B_{1} = A_{1} C_{1}$ ， D，E分别是棱BC， $C C_{1}$ 上的点（点D不同于点C），且 $A D ⊥ D E$ ， F为 $B_{1} C_{1}$ 的中点.

求证：

(1)、平面 $A D E ⊥$ 平面 $B C C_{1} B_{1}$ ；

(2)、直线 $A_{1} F ∥$ 平面ADE.

查看试题解析
19. 在 $△ A B C$ 中，设角A，B，C的对边长分别为a，b，c，已知 $\frac{s i n A - s i n B}{s i n C} = \frac{a - c}{a + b}$ .

(1)、求角B的值；

(2)、若 $△ A B C$ 为锐角三角形，且 $c = 2$ ，求 $△ A B C$ 的面积S的取值范围.

查看试题解析
20. 已知函数 $f (x) = x^{2} + b x + c (b ， c \in R)$ 的图象过点 $(1 ， 0)$ ，且对 $\forall x \in R$ ， $f (2 - x) = f (2 + x)$ 恒成立.

(1)、求函数 $f (x)$ 的解析式；

(2)、若对任意的 $x \in [\frac{1}{e^{2}} ， e^{4}]$ ，不等式 $f (l n x) \geq m l n x$ 恒成立，求m的最小值.（其中 $e \approx 2.71828$ 是自然对数的底数）

查看试题解析
21. 已知面积为 $2 \sqrt{3}$ 的菱形ABCD如图①所示，其中 $A C = 2$ ， E是线段AD的中点.现将 $△ D A C$ 沿AC折起，使得点D到达点S的位置.

(1)、若二面角 $S - A C - B$ 的平面角大小为 $\frac{2 π}{3}$ ，求三棱锥 $S - A B C$ 的体积；

(2)、若二面角 $S - A C - B$ 的平面角 $α \in [\frac{π}{3} ， \frac{2 π}{3}]$ ，点F在三棱锥的表面运动，且始终保持 $E F ⊥ A C$ ，求点F的轨迹长度的取值范围.

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $A B ⊥ A C$ ， $2 A C = 3 A B = 6$ ， D，E，F分别在线段AC，AB，BC上，满足 $C D = 2 D A$ 且 $D E ⊥ D F$ ，记 $∠ A E D = α$ .

(1)、用含 $α$ 的代数式表示 $s i n ∠ D F C$ ；

(2)、求 $△ D E F$ 面积的最小值.

查看试题解析