广东省深圳市龙岗区2022-2023学年七年级下册期末考试数学试卷
试卷更新日期:2023-07-05 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
-
1. 计算:的结果是( )A、2 B、-2 C、 D、2. 下列图中和是对顶角的是( )A、
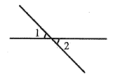 B、
B、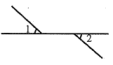 C、
C、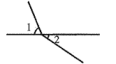 D、
D、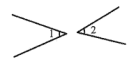 3. 2023奥港澳大湾区花展于4月8日至17日在深圳市仙湖植物园和分会场香蜜湖四季花谷举行.本届花展以“鲜花与梦想”为主题,以杜鹃花为主题花,表达湾区都市生活的唯美与浪漫,展现深圳梦想之都的活力与热情.杜鹃花的花粉直径约为0.000035米,则0.000035米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 若干条直线(或线段)按一定的方式排列可以“围”出各种美丽的图形,我们形象的把它们称为“数学刺绣”,下列“数学刺绣”图案中,不是轴对称图形的是( )A、
3. 2023奥港澳大湾区花展于4月8日至17日在深圳市仙湖植物园和分会场香蜜湖四季花谷举行.本届花展以“鲜花与梦想”为主题,以杜鹃花为主题花,表达湾区都市生活的唯美与浪漫,展现深圳梦想之都的活力与热情.杜鹃花的花粉直径约为0.000035米,则0.000035米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 若干条直线(或线段)按一定的方式排列可以“围”出各种美丽的图形,我们形象的把它们称为“数学刺绣”,下列“数学刺绣”图案中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,已知 , 要得到 , 则不能添加的条件是( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,已知 , 要得到 , 则不能添加的条件是( ) A、 B、 C、 D、7. 地表以下岩层的湿度随着所处深度的变化而变化,在某个地点与的部分对应数据如下表,则该地y与x的函数关系可以近似的表示为
A、 B、 C、 D、7. 地表以下岩层的湿度随着所处深度的变化而变化,在某个地点与的部分对应数据如下表,则该地y与x的函数关系可以近似的表示为所处深度
2
3
5
7
10
13
地表以下岩层的温度
90
125
195
265
370
475
则该地y与x的关系可以近似的表示为( )
A、 B、 C、 D、8. 下列说法正确的有( )①任意投掷一枚质地均匀的硬币30次,出现正面朝上的次数一定是15次;
②小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是;

③“三角形任意两边之和大于第三边”这一事件是必然事件;
④某路口的红绿灯设置为红灯40s,绿灯60s,黄灯3s,则小明遇见红灯的概率是.
A、1个 B、2个 C、3个 D、4个9. 【观察】①;②;
③;
……
【归纳】由此可得:;
【应用】请运用上面的结论,计算:( )
A、 B、 C、 D、10. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
 A、1m B、1.6m C、 D、
A、1m B、1.6m C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 计算: .12. 在学校组织的“广东美食推荐”活动中,小明所在组的题目设置为“肠粉”、“煲仔饭”、“烧鹅”、“云吞面”,小明从中随机抽取一个进行介绍,恰好抽到“肠粉”的概率是.13. 如图,一根直尺和一个含的直角三角板按如图方式叠合在一起(三角板的直角顶点在直尺的边上),若 , 则的度数是.
 14. 在中,是AC边上的高, , 则的度数为°.15. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
14. 在中,是AC边上的高, , 则的度数为°.15. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
三、解答题(本题共7小题,共55分)
-
16. 计算:(1)、(2)、(3)、17. 先化简,再求值: , 其中.18. 下图是某种晶体熔化(晶体由固态到液态的过程)时温度随时间变化的图象.
 (1)、这一变化过程中,自变量是 , 因变量是.(2)、晶体从开始熔化到熔化结束的过程中保持温度不变,这一温度称为晶体的熔点.该晶体熔点为 , 熔化过程大约持续了;19. 下表是某校生物兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
(1)、这一变化过程中,自变量是 , 因变量是.(2)、晶体从开始熔化到熔化结束的过程中保持温度不变,这一温度称为晶体的熔点.该晶体熔点为 , 熔化过程大约持续了;19. 下表是某校生物兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:试验的种子数
100
200
500
1000
2000
5000
发芽的粒数
94
475
954
1906
4748
发芽频率
0.94
0.955
0.946
0.953
0.9496
(1)、上表中的a= , b=.(2)、任取一粒这种植物种子,它能发芽的概率的估计值是(精确到0.01);(3)、若该校劳动基地需要这种植物幼苗9500棵,试估算需要准备多少粒种子进行发芽培育.20. 如图,在中. (1)、实践与操作:作AB的垂直平分线,交BC于 , 交AB于;(要求:尺规作图并保留作图痕迹,不写作法,标明字母)(2)、推理与计算:在(1)的条件下,连接AD,若 , 求的度数.21. 综合与实践
(1)、实践与操作:作AB的垂直平分线,交BC于 , 交AB于;(要求:尺规作图并保留作图痕迹,不写作法,标明字母)(2)、推理与计算:在(1)的条件下,连接AD,若 , 求的度数.21. 综合与实践【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点是BC边上的中点,连接AD.求证:.

证明:过点作于
(1)、【拓展探究】如图2,在△ABC中,点D是BC边上的中点中,点是BC边上的中点,若 , 则.
 (2)、如图3,在中,点是BC边上的点且和存在怎样的数量关系?请模仿写出证明过程.
(2)、如图3,在中,点是BC边上的点且和存在怎样的数量关系?请模仿写出证明过程. (3)、【问题解决】
(3)、【问题解决】现在有一块四边形土地ABCD(如图4),能大和熊二都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.

要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
22.(1)、如图1,在中,是BC边上一点,且 , 若 , 则. (2)、如图2,在中,是BC边上一点, , 点在线段AD上且 , 求证:.
(2)、如图2,在中,是BC边上一点, , 点在线段AD上且 , 求证:. (3)、如图3,在中,是CB延长线上一点, , 点在射线DA上且 , 请画出点的位置,此时AB和CE满足怎样的数量关系,请说明理由.
(3)、如图3,在中,是CB延长线上一点, , 点在射线DA上且 , 请画出点的位置,此时AB和CE满足怎样的数量关系,请说明理由.