浙教版数学八年级上册2.2-2.3等腰三角形的性质 同步测试(提高版)
试卷更新日期:2023-07-05 类型:同步测试
一、选择题
-
1. 如图,在ABC中,AB=AC,AD平分∠BAC,则下列结论错误的是( )
 A、∠B=∠C B、AD⊥BC C、∠BAD=∠CAD=∠C D、BD=CD2. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( )
A、∠B=∠C B、AD⊥BC C、∠BAD=∠CAD=∠C D、BD=CD2. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( ) A、2 B、3 C、4 D、53. 如图,在等腰三角形ABC中,AB=AC=4,∠BAC=30°,AG是底边BC上的高.在AG的延长线上有一个动点D,连接CD,作∠CDE=150°,交AB的延长线于点E,∠CDE的角平分线交AB边于点F,则在点D运动的过程中,线段EF的最小值( )
A、2 B、3 C、4 D、53. 如图,在等腰三角形ABC中,AB=AC=4,∠BAC=30°,AG是底边BC上的高.在AG的延长线上有一个动点D,连接CD,作∠CDE=150°,交AB的延长线于点E,∠CDE的角平分线交AB边于点F,则在点D运动的过程中,线段EF的最小值( ) A、6 B、4 C、3 D、24. 如图,在中,按以下步骤作图:分别以为圆心,大于的长为半径作弧,两相交于两点;②作直线交于点 , 连接.若.则的度数为( )
A、6 B、4 C、3 D、24. 如图,在中,按以下步骤作图:分别以为圆心,大于的长为半径作弧,两相交于两点;②作直线交于点 , 连接.若.则的度数为( ) A、 B、 C、 D、5. 如图,在△ABC中,AB=AC,∠A=40°,E为AB上一点,D为BC延长线上一点,连接DE,交AC于点F,过点E作EG∥BC交AC于点G.若CF=GF,∠D=35°,则下列结论错误的是( )
A、 B、 C、 D、5. 如图,在△ABC中,AB=AC,∠A=40°,E为AB上一点,D为BC延长线上一点,连接DE,交AC于点F,过点E作EG∥BC交AC于点G.若CF=GF,∠D=35°,则下列结论错误的是( ) A、CD=EG B、DF=EF C、CD=CF D、BD=DE6. 如图,已知等腰三角形 , , 若以点B为圆心,长为半径画弧,交腰于点E,则下列结论一定正确的是( )
A、CD=EG B、DF=EF C、CD=CF D、BD=DE6. 如图,已知等腰三角形 , , 若以点B为圆心,长为半径画弧,交腰于点E,则下列结论一定正确的是( ) A、 B、 C、 D、7. 在平面直角坐标系中,已知点 , 在坐标轴上确定一点B,使为等腰三角形,则符合条件的点B共有( )A、5个 B、6个 C、7个 D、8个8. 如图,在△ABC中,∠C=85°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,交BC于点D,连接AD,则∠CAD的度数为( )
A、 B、 C、 D、7. 在平面直角坐标系中,已知点 , 在坐标轴上确定一点B,使为等腰三角形,则符合条件的点B共有( )A、5个 B、6个 C、7个 D、8个8. 如图,在△ABC中,∠C=85°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,交BC于点D,连接AD,则∠CAD的度数为( ) A、50° B、45° C、35° D、30°9. 如图所示的正方形网格中,网格的交点称为格点,已知 , 是两格点,如果也是图中的格点,且使得为等腰三角形,则符合条件的点的个数是( )
A、50° B、45° C、35° D、30°9. 如图所示的正方形网格中,网格的交点称为格点,已知 , 是两格点,如果也是图中的格点,且使得为等腰三角形,则符合条件的点的个数是( ) A、9 B、8 C、7 D、610. 如图,在△ABC中,AB=AC,AD是高线,E是AB的中点,已知△ABC的面积为8,则△ADE的面积为( )
A、9 B、8 C、7 D、610. 如图,在△ABC中,AB=AC,AD是高线,E是AB的中点,已知△ABC的面积为8,则△ADE的面积为( )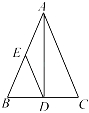 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .12. 如图,等腰的底边长为4,面积是16,腰的垂直平分线分别交 , 边于E,F点,若点D为边的中点,点M为线段上一动点,则周长的最小值为.
 13. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.
13. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.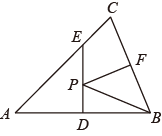 14. 如图,小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°.
14. 如图,小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°. 15. 如图,已知点P是射线上一动点, , 当为时,是等腰三角形.
15. 如图,已知点P是射线上一动点, , 当为时,是等腰三角形. 16. 等腰中, , 平分 , 若 , 则 .
16. 等腰中, , 平分 , 若 , 则 .
三、综合题
-
17. 已知是等腰三角形的两条边,且 , 求这个三角形的周长.18. 如图,已知在中, , , , 请在三角形的边上找一点 , 并过点和三角形的一个顶点画一条线段,将这个三角形分成两个等腰三角形.要求两种不同的分法并写出每个等腰三角形的内角度数
 19. 如图,点D、E在的边上, , , 求证:.
19. 如图,点D、E在的边上, , , 求证:. 20. 如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线DE分别交AB,AC于点D,E.
20. 如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线DE分别交AB,AC于点D,E.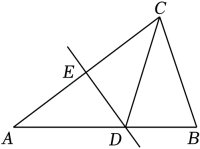 (1)、求证:△BCD是等腰三角形;(2)、若△BCD的周长是13,BC=5,求AC的长.21. 如图,在△ABC中,AB=AC,∠B=50°,D是边BC上的一个动点(点D不与点B,C重合),连接AD,作∠ADE=50°,DE与AC相交于点E.
(1)、求证:△BCD是等腰三角形;(2)、若△BCD的周长是13,BC=5,求AC的长.21. 如图,在△ABC中,AB=AC,∠B=50°,D是边BC上的一个动点(点D不与点B,C重合),连接AD,作∠ADE=50°,DE与AC相交于点E. (1)、当BD=CE时,求证:△ABD≌△DCE ;(2)、当△ADE是等腰三角形时,求∠BAD的度数.22. 如图,在中,已知 , 是边上的中线,点是边上一动点,点是上的一个动点.
(1)、当BD=CE时,求证:△ABD≌△DCE ;(2)、当△ADE是等腰三角形时,求∠BAD的度数.22. 如图,在中,已知 , 是边上的中线,点是边上一动点,点是上的一个动点.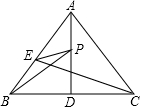 (1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.23. 综合与实践
(1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.23. 综合与实践在等腰三角形纸片中, , . 现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应的任务.
作法:如图1.
①分别作 , 的垂直平分线,交于点P;
②连接 , ,
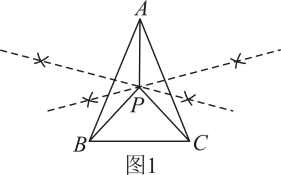
结论:沿线段 , , 剪开,即可得到三个等腰三角形
理由:∵点P在线段的垂直平分线上,
∴____.(依据)
同理,得
∴
∴ , , 都是等腰三角形.
任务:
(1)、上述过程中,横线上的结论为 , 括号中的依据为 .(2)、受小文的启发,同学们想到另一种思路:如图2,以点B为圆心,长为半径作弧,交于点D,交于点E.在此基础上构造两条线段(以图中标有字母的点为端点)作为裁剪线,也可解决问题.请在图2中画出一种裁剪方案,并求出得到的三个等腰三角形及相应顶角的度数. (3)、如图3,在等腰三角形纸片中, , . 请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形.(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线)
(3)、如图3,在等腰三角形纸片中, , . 请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形.(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线)