2023年浙教版数学八年级上册2.1轴对称图形同步测试（培优版）

试卷更新日期：2023-07-05 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，正八边形是轴对称图形，对称轴可以是直线（）

A、 $a$ B、 $b$ C、 $c$ D、 $d$

查看试题解析
2. 下列轴对称图形中，对称轴条数最多的是（）

A、等边三角形 B、菱形 C、等腰梯形 D、圆

查看试题解析
3. 苏州的景色非常优美，其中以苏州园林最具代表性.苏州园林溯源于春秋，发展于晋唐，繁荣于两宋，全胜于明清，现存五十多处.如图是苏州园林中的一种窗格，下面从窗格图案中提取的几何图形，不一定是轴对称图形的是（）

A、矩形 B、正八边形 C、平行四边形 D、等腰三角形

查看试题解析
4. 小颖的爸爸要在某条街道l上修建一个奶站P，向居民区A，B提供牛奶，要使点P到A，B的距离之和最短，则下列作法正确的是（）

A、 B、 C、 D、

查看试题解析
5. 我们在观看台球比赛时，发现选手们常常会用反弹的技巧击打目标球．在此过程中，撞击路线与桌边的夹角等于反射路线与桌边的夹角，如图1， $∠ 1 = ∠ 2$ ．如图2，建立平面直角坐标系 $x O y$ ，已知A球位于点 $(1 ， 2)$ 处，B球位于点 $(6 ， 1)$ 处．现击打A球，使A球向桌边的整点位置（横纵坐标均为整数，球洞位置不可反弹）撞击，若A球最多在台球桌边反弹两次后击中B球，则满足条件的桌边整点有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ， $B D$ 平分 $∠ A B C$ ，点E是 $B C$ 的中点，点P是 $B D$ 上一动点，连接 $P C ， P E$ ，若 $B C = 6$ ， $A B = 10$ ， $S_{△ A B C} = 15 \sqrt{3}$ ，则 $P C + P E$ 的最小值是（）

A、 $3 \sqrt{3}$ B、6 C、 $5 \sqrt{3}$ D、10

查看试题解析
7. 如图，在 $3 \times 3$ 的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的 $△ A B C$ 为格点三角形，在图中最多能画出（）个格点三角形与 $△ A B C$ 成轴对称.

A、6 B、5 C、4 D、3

查看试题解析
8. 如图，在△ABC中，AB＝AC．在AB、AC上分别截取AP、AQ，使AP＝AQ．再分别以点P，Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠BAC内交于点R，作射线AR，交BC于点D．已知BC＝5，AD=6．若点M、N分别是线段AD和线段AC上的动点，则CM+MN的最小值为（）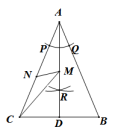

A、4 B、5 C、 $\frac{60}{13}$ D、2 $\sqrt{6}$

查看试题解析
9. 如图，∠AOB=20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记∠MPQ= $α$ ，∠PQN= $β$ ，当MP+PQ+QN最小时，则 $β - α$ 的值为（）

A、10° B、20° C、40° D、60°

查看试题解析
10. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点D，E，F分别是 $A D$ ， $A C$ 边上的动点，则 $C E + E F$ 的最小值为（）

A、 $\frac{24}{5}$ B、 $\frac{12}{5}$ C、 $\frac{6}{5}$ D、 $\frac{18}{5}$

查看试题解析

二、填空题

11. 如图，桌球的桌面上有M，N两个球，若要将M球射向桌面的一边，反弹一次后击中N球，则A，B，C，D，4个点中，可以反弹击中N球的是点.

查看试题解析
12. 如图，点P为 $∠ A O B$ 内一点，分别作出P点关于 $O B$ 、 $O A$ 的对称点 $P_{1}$ ， $P_{2}$ ，连接 $P_{1} P_{2}$ 交 $O B$ 于M，交 $O A$ 于N，若 $∠ A O B = 40 °$ ，则 $∠ M P N$ 的度数是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 6$ ， $B C = 7$ ， $E F$ 垂直平分 $B C$ ，点 $D$ 为直线 $E F$ 上的一个动点，则 $△ A B D$ 周长的最小值是。

查看试题解析
14. 如图，Rt△ABC中，∠C＝ $9 0^{°}$ ， AC＝6，BC＝8，AB＝10，EF垂直平分AB，点P为直线EF上一动点，则△APC周长的最小值为．

查看试题解析
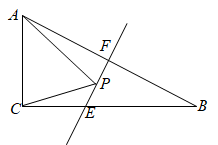15. 如图的4×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC全等的格点三角形一共有个．

查看试题解析

三、综合题

16. 如图，亮亮在A处看护羊群吃草，其家在B处，A，B到河岸的距离分别为AC=200m，BD=100m，CD=400m，亮亮从A处把羊群赶到河边饮水后回家，作图说明亮亮如何行走路程最短，并求出亮亮走的最短路程．

查看试题解析
17. 在 $6 \times 6$ 的网格中已经涂黑了三个小正方形，请在图中涂黑一块（或两块）小正方形，使涂黑的四个（或五个）小正方形组成一个轴对称图.

查看试题解析
18. 已知 $∠ A O B = 30 °$ ，点P在 $∠ A O B$ 的内部，点C和点P关于OA对称，点P关于OB的对称点是D，连接CD交OA于M，交OB于N， $C D = 15$ ．

(1)、补全图，并且保留作图痕迹．

(2)、写出∠COD°．△PMN的周长为．

查看试题解析
19. 如图，网格中的△ABC与△DEF为轴对称图形．

(1)、利用网格线画出△ABC与△DEF的对称轴l；

(2)、结合所画图形，在直线l上画出点P，使PA+PC最小，并说明你的理由；

(3)、如果每一个小正方形的边长为1，请直接写出△ABC的面积＝．

查看试题解析
20. 如图，在正方形网格中，每个小正方形的边长均相等， $△ A B C$ 的三个顶点A，B，C都在格点上．

(1)、在图中画出与 $△ A B C$ 关于直线l成轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、在直线l上找出一点Q，使得 $| Q A + Q C |$ 的值最小；（描出该点并标注字母Q）

(3)、在直线l上找出一点P，使得 $| P A - P C |$ 的值最大．（保留作图痕迹并标注点P）

查看试题解析
21.

(1)、画图探究：如图①，若点 $A$ ， $B$ 在直线 $m$ 的同侧，在直线 $m$ 上求作一点 $P$ ，使 $A P + B P$ 的值最小，保留作图痕迹，不写作法；

(2)、实践运用：如图②，等边 $△ A B C$ 的边 $B C$ 上的高为6， $A D$ 是边 $B C$ 上的中线， $M$ 是 $A D$ 上的动点， $E$ 是 $A C$ 的中点，求 $E M + C M$ 的最小值．

查看试题解析
22. 如图①，OP是∠MON的平分线，请你利用该图画一对以OP所在直线为对称轴的全等三角形．参考这个作全等三角形的方法，解答下列问题：

(1)、如图②，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．求∠EFA的度数；

(2)、在（1）的条件下，请你判断FE与FD之间的数量关系，并说明道理．

(3)、如图③，在△ABC中，如果∠ACB不是直角，而（1）中的其它条件不变，请问，你在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

查看试题解析

2023年浙教版数学八年级上册2.1轴对称图形 同步测试（培优版）

一、选择题

二、填空题

三、综合题

2023年浙教版数学八年级上册2.1轴对称图形同步测试（培优版）