广东省深圳市宝安区2022-2023学年七年级下册期末考试数学试卷
试卷更新日期:2023-07-04 类型:期末考试
一、选择题(共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的,请把答案按要求填涂到答题卡相应位置上)
-
1. 的值是( )A、 B、 C、 D、2. 以下是“有机食品”、“安全饮品”、“循环再生”、“绿色食品”的四个标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. PM2.5是指大气中直径小于或等于(表示微米,)的颗粒物,也称为可入肺颗粒物.科学家用PM2.5表示每立方米空气中这种颗粒的含量,值越高,代表空气污染越严重.将用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 一个不透明的袋中装有4个白球,若干个红球,这些球除颜色外完全相同.通过多次摸球实验后发现,摸到白球的频率稳定在0.4附近,则袋中红球的个数是( )A、2 B、5 C、6 D、106. 等腰三角形的一边长 , 另一边长 , 它的第三边长为( )A、 B、 C、 D、或7. 一个圆的半径为 , 增加3cm后,这个圆的面积增加了( )A、 B、 C、 D、8. 小明为了检测甲、乙两品牌儿童水杯的保温性能,从甲、乙两个品牌中各取一个容积相同的水杯进行实验:同时装满相同温度的水,每隔一段时间分别测量一次两个水杯的水温(实验过程中室温保持不变),最后小明把记录的温度绘制成如图所示的图象,观察图象,下列说法中错误的是( )
3. PM2.5是指大气中直径小于或等于(表示微米,)的颗粒物,也称为可入肺颗粒物.科学家用PM2.5表示每立方米空气中这种颗粒的含量,值越高,代表空气污染越严重.将用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 一个不透明的袋中装有4个白球,若干个红球,这些球除颜色外完全相同.通过多次摸球实验后发现,摸到白球的频率稳定在0.4附近,则袋中红球的个数是( )A、2 B、5 C、6 D、106. 等腰三角形的一边长 , 另一边长 , 它的第三边长为( )A、 B、 C、 D、或7. 一个圆的半径为 , 增加3cm后,这个圆的面积增加了( )A、 B、 C、 D、8. 小明为了检测甲、乙两品牌儿童水杯的保温性能,从甲、乙两个品牌中各取一个容积相同的水杯进行实验:同时装满相同温度的水,每隔一段时间分别测量一次两个水杯的水温(实验过程中室温保持不变),最后小明把记录的温度绘制成如图所示的图象,观察图象,下列说法中错误的是( ) A、4h时,甲品牌水杯水温较高 B、8h时,甲、乙两品牌水杯水温相同 C、甲、乙两品牌水杯水温都随着时间的增加而降低 D、8h以后,乙品牌水杯水温下降更快9. 下列说法正确的是( )A、三角形的三条中线、三条高都在三角形内部 B、成轴对称的两个图形,对应点所连线段被对称轴垂直平分 C、一个锐角和一条边分别相等的两个直角三角形全等 D、小凡做了100次抛掷均匀硬币的实验,其中52次正面朝上,48次正面朝下,则正面朝上的概率为0.5210. 如图,长方形中,点为上一点,连接 , 将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、 , 若、、 , 则的最小值是( )
A、4h时,甲品牌水杯水温较高 B、8h时,甲、乙两品牌水杯水温相同 C、甲、乙两品牌水杯水温都随着时间的增加而降低 D、8h以后,乙品牌水杯水温下降更快9. 下列说法正确的是( )A、三角形的三条中线、三条高都在三角形内部 B、成轴对称的两个图形,对应点所连线段被对称轴垂直平分 C、一个锐角和一条边分别相等的两个直角三角形全等 D、小凡做了100次抛掷均匀硬币的实验,其中52次正面朝上,48次正面朝下,则正面朝上的概率为0.5210. 如图,长方形中,点为上一点,连接 , 将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、 , 若、、 , 则的最小值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共15分,请把答案填到答题卡相应位置上)
-
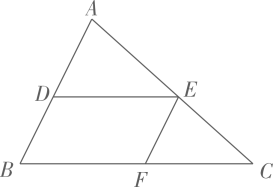
11. 若 , 则.12. 如图, , , , , 则.
 13. 如图,在一个面积为的等边三角形纸片中,取三边的中点,以虚线为折痕折叠纸片,图中阴影部分的面积为.
13. 如图,在一个面积为的等边三角形纸片中,取三边的中点,以虚线为折痕折叠纸片,图中阴影部分的面积为. 14. 乐乐设计了一个有趣的运算程序:任意写出一个三位数(三位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差.重复这个过程……以579开始,按照此程序运算6次后得到的数是.15. 如图,中, , 点为延长线上一点,于点 , 点为延长线上一点,连接交的延长线于点 , 点是的中点,若 , , 则.
14. 乐乐设计了一个有趣的运算程序:任意写出一个三位数(三位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差.重复这个过程……以579开始,按照此程序运算6次后得到的数是.15. 如图,中, , 点为延长线上一点,于点 , 点为延长线上一点,连接交的延长线于点 , 点是的中点,若 , , 则.
三、解答题(本题共7小题,其中第16题10分,第17题6分,第18题8分,第19题6分,第20题6分,第21题9分,第22题10分,共55分)
-
16. 计算:(1)、(2)、17. 先化简,再求值: , 其中 , .18. 如图,在中,是边上一点,是边上一点,连接.
 (1)、过点作的平行线,与的延长线交于点(尺规作图,不写作法,保留作图痕迹);(2)、若是的中点,求证:.19. 小明和小颖用一副去掉大、小王的扑克牌(共52张)做摸牌游戏:小明从中任意抽取一张牌(不放回),小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关),然后两人把摸到的牌都放回,重新开始游戏。(1)、若小明已经摸到的牌面为6,然后小颖摸牌,那么小明获胜的概率是;(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是;(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是.20. 如图,在长为20cm,宽为16cm的长方形四个角上,分别剪去四个全等的等腰直角三角形,当三角形的直角边的长度变化时,阴影部分的面积也随之发生变化.设剪去的每个三角形的直角边长为 , 阴影部分的面积为.
(1)、过点作的平行线,与的延长线交于点(尺规作图,不写作法,保留作图痕迹);(2)、若是的中点,求证:.19. 小明和小颖用一副去掉大、小王的扑克牌(共52张)做摸牌游戏:小明从中任意抽取一张牌(不放回),小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关),然后两人把摸到的牌都放回,重新开始游戏。(1)、若小明已经摸到的牌面为6,然后小颖摸牌,那么小明获胜的概率是;(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是;(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是.20. 如图,在长为20cm,宽为16cm的长方形四个角上,分别剪去四个全等的等腰直角三角形,当三角形的直角边的长度变化时,阴影部分的面积也随之发生变化.设剪去的每个三角形的直角边长为 , 阴影部分的面积为.三角形的直角边长/cm
1
2
3
4
…
阴影部分的面积
312
288
…
 (1)、表中的数据 , ;(2)、当等腰直角三角形的直角边长由4增加到7时,阴影部分的面积(填增大或减小);(3)、写出与的关系式.21. 随着科技的发展,在公共区域内安装“360°智能全景摄像头”成为保护人民生命财产安全的有效手段。如图1所示,这是某仓库的平面图,点是图形内任意一点,点是图形内的点,连接 , 若线段总是在图形内或图形上,则称是“完美观测点”,此处便可安装摄像头,而不是“完美观测点”.
(1)、表中的数据 , ;(2)、当等腰直角三角形的直角边长由4增加到7时,阴影部分的面积(填增大或减小);(3)、写出与的关系式.21. 随着科技的发展,在公共区域内安装“360°智能全景摄像头”成为保护人民生命财产安全的有效手段。如图1所示,这是某仓库的平面图,点是图形内任意一点,点是图形内的点,连接 , 若线段总是在图形内或图形上,则称是“完美观测点”,此处便可安装摄像头,而不是“完美观测点”.

 (1)、如图2,以下各点是完美观测点的是____(只有一个选项是正确的)A、 B、 C、 D、(2)、如图3,在图形内作出两个完美观测点,并分别用字母、表示;(3)、图4是某景观大楼的平面图,请作出该图形中由所有“完美观测点”组成的图形,并用阴影表示.22. “等面积法”是解决三角形内部线段长度的常用方法.如图1,在中, , 作 , 若 , , , 可列式: , 解得.
(1)、如图2,以下各点是完美观测点的是____(只有一个选项是正确的)A、 B、 C、 D、(2)、如图3,在图形内作出两个完美观测点,并分别用字母、表示;(3)、图4是某景观大楼的平面图,请作出该图形中由所有“完美观测点”组成的图形,并用阴影表示.22. “等面积法”是解决三角形内部线段长度的常用方法.如图1,在中, , 作 , 若 , , , 可列式: , 解得. (1)、在题干的基础上,
(1)、在题干的基础上,①如图2,点为上一点,作 , , 设 , , 求证:;
②如图3,当点在延长线上时,猜想、之间又有什么样的数量关系,请证明你的猜想;
(2)、如图4,在中, , , .若点是延长线上一点,且 , 过点作 , 点是直线上一动点,点是直线上一动点,连接、 , 求的最小值.