湖南省岳阳市汨罗市2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-04 类型:期中考试
一、单选题
-
1. 下列环保标志,既是轴对称图形,也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在中, , , 则的度数为( )A、° B、 C、 D、3. 已知点与关于x轴对称,则( )A、1 B、0 C、4 D、24. 如图,是中的角平分线,于点E, , 则的长是( )
2. 在中, , , 则的度数为( )A、° B、 C、 D、3. 已知点与关于x轴对称,则( )A、1 B、0 C、4 D、24. 如图,是中的角平分线,于点E, , 则的长是( ) A、3 B、4 C、6 D、55. 如图,四边形ABCD的对角线交于点O , 下列哪组条件不能判断四边形ABCD是平行四边形( )
A、3 B、4 C、6 D、55. 如图,四边形ABCD的对角线交于点O , 下列哪组条件不能判断四边形ABCD是平行四边形( ) A、OA=OC , OB=OD B、AB=CD , AO=CO C、AB=CD , AD=BC D、∠BAD=∠BCD , AB∥CD6. 下列条件,不能判定两个直角三角形全等的是( )A、两个锐角对应相等 B、一个锐角和斜边对应相等 C、两条直角边对应相等 D、一条直角边和斜边对应相等7. 一个等边三角形和两个等腰直角三角形的位置如图所示,若∠3=70°,则∠1+∠2=( )
A、OA=OC , OB=OD B、AB=CD , AO=CO C、AB=CD , AD=BC D、∠BAD=∠BCD , AB∥CD6. 下列条件,不能判定两个直角三角形全等的是( )A、两个锐角对应相等 B、一个锐角和斜边对应相等 C、两条直角边对应相等 D、一条直角边和斜边对应相等7. 一个等边三角形和两个等腰直角三角形的位置如图所示,若∠3=70°,则∠1+∠2=( )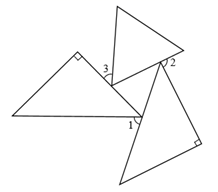 A、290° B、200° C、140° D、110°8. 如图,在平面直角坐标系上有点A(1,-1),点A第一次向左跳动至A1(-1,0),第二次向右跳动至A2(2,0),第三次向左跳动至A3(-2,1),第四次向右跳动至A4(3,1)…依照此规律跳动下去,点A第9次跳动至A9的坐标( )
A、290° B、200° C、140° D、110°8. 如图,在平面直角坐标系上有点A(1,-1),点A第一次向左跳动至A1(-1,0),第二次向右跳动至A2(2,0),第三次向左跳动至A3(-2,1),第四次向右跳动至A4(3,1)…依照此规律跳动下去,点A第9次跳动至A9的坐标( )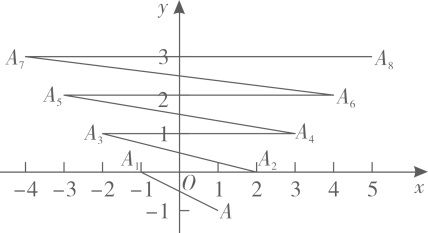 A、(-5,4) B、(-5,3) C、(6,4) D、(6,3)
A、(-5,4) B、(-5,3) C、(6,4) D、(6,3)二、填空题
-
9. 若一个多边形的外角和是其内角和的 , 则此多边形的边数为 .10. 若直角三角形的两条直角边分别5和12,则斜边上的中线长为 .11. 在高5m,长13m的一段台阶上铺上地毯,台阶的剖面如图所示,地毯的长度至少需要 m.
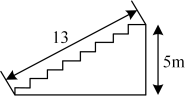 12. 如图所示,某居民小区为了美化居住环境,要在一块等边三角形空地上围一个四边形花坛.已知四边形的顶点E,F分别是边 , 的中点,量得米, , 则四边形花坛的周长是 .
12. 如图所示,某居民小区为了美化居住环境,要在一块等边三角形空地上围一个四边形花坛.已知四边形的顶点E,F分别是边 , 的中点,量得米, , 则四边形花坛的周长是 .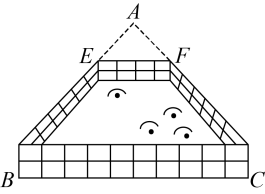 13. 如图,湖边有三条公路,其中公路互相垂直,公路的中点M与点C被湖隔开.测得的长为 , 则M,C两点间的距离为 .
13. 如图,湖边有三条公路,其中公路互相垂直,公路的中点M与点C被湖隔开.测得的长为 , 则M,C两点间的距离为 . 14. 如图,在△=度.
14. 如图,在△=度. 15. 顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是 .16. 如图,正方形和正方形的顶点A,E,O在同一直线l上,且 , , 得出下列结论:① , ②的面积为 .
15. 顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是 .16. 如图,正方形和正方形的顶点A,E,O在同一直线l上,且 , , 得出下列结论:① , ②的面积为 .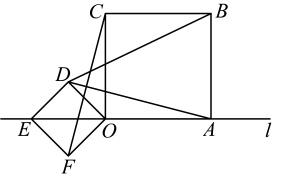
三、解答题
-
17. 为的高,相交于H点, , 求 .
 18. 出△ABC关于y轴对称的图形△A1B1C1 . 求:
18. 出△ABC关于y轴对称的图形△A1B1C1 . 求: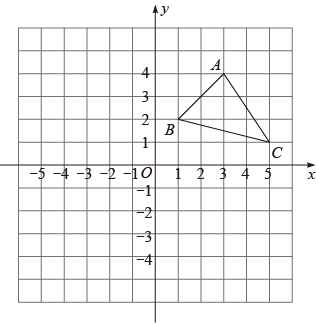 (1)、△A1B1C1三个顶点的坐标.(2)、△A1B1C1的面积.19. 图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足 , 现测得dm,dm,dm,其中与之间由一个固定为90°的零件连接(即),通过计算说明该车是否符合安全标准.
(1)、△A1B1C1三个顶点的坐标.(2)、△A1B1C1的面积.19. 图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足 , 现测得dm,dm,dm,其中与之间由一个固定为90°的零件连接(即),通过计算说明该车是否符合安全标准. 20. 如图,在中,对角线 , 交于点O,点E,F分别是 , 的中点,连接 , , 求证: .
20. 如图,在中,对角线 , 交于点O,点E,F分别是 , 的中点,连接 , , 求证: . 21. 如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.
21. 如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°. 22. 如图,A、B两点分别在射线上,点C在的内部,且 , , 垂足分别为D,E,且 .
22. 如图,A、B两点分别在射线上,点C在的内部,且 , , 垂足分别为D,E,且 . (1)、求证:平分;(2)、若 , 求的长.23. 如图1,把直角三角形MON的直角顶点O 放在直线AB上,射线 OC平分∠AON .
(1)、求证:平分;(2)、若 , 求的长.23. 如图1,把直角三角形MON的直角顶点O 放在直线AB上,射线 OC平分∠AON . (1)、观察分析:
(1)、观察分析:
如图1,若∠MOC=28°,则∠BON的度数为;(2)、若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,求∠MOC 的度数.(3)、猜想探究:若将三角形 MON绕点O旋转到如图3所示的位置,请你猜想∠BON和∠MOC之间的数量关系,并说明理由.24. 如图,▱ABCD中,AB=2cm,AC=5cm,S▱ABCD=8cm2 , E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒. (1)、在运动过程中,四边形AECF的形状是;(2)、t=时,四边形AECF是矩形;(3)、求当t等于多少时,四边形AECF是菱形.
(1)、在运动过程中,四边形AECF的形状是;(2)、t=时,四边形AECF是矩形;(3)、求当t等于多少时,四边形AECF是菱形.