湖南省长沙市宁乡市西部乡镇联考2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-04 类型:期中考试
一、单选题
-
1. 下列图形分别是平行四边形、矩形、菱形、正方形,其中不一定是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在▱ABCD 中,若∠A+∠C=130°,则∠D 的大小为( )
2. 如图,在▱ABCD 中,若∠A+∠C=130°,则∠D 的大小为( ) A、100° B、105° C、110° D、115°3. 下列各式中,运算正确的是( )A、 B、 C、 D、4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、1, , B、3,4,5 C、5,12,13 D、2,2,36. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )
A、100° B、105° C、110° D、115°3. 下列各式中,运算正确的是( )A、 B、 C、 D、4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、1, , B、3,4,5 C、5,12,13 D、2,2,36. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )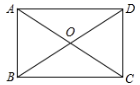 A、4 B、 C、3 D、57.
A、4 B、 C、3 D、57.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
 A、平行四边形 B、矩形 C、菱形 D、正方形8.
A、平行四边形 B、矩形 C、菱形 D、正方形8.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
 A、16 B、15 C、14 D、139. 下列命题中,正确的是( )A、有一组邻边相等的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、两组邻角相等的四边形是平行四边形 D、对角线互相垂直且相等的平行四边形是正方形10. 如图,在 中对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为(...)
A、16 B、15 C、14 D、139. 下列命题中,正确的是( )A、有一组邻边相等的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、两组邻角相等的四边形是平行四边形 D、对角线互相垂直且相等的平行四边形是正方形10. 如图,在 中对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为(...) A、10 B、8 C、6 D、411. 如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A、10 B、8 C、6 D、411. 如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )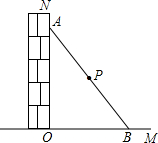 A、变小 B、不变 C、变大 D、无法判断12. 如图,点为矩形的边长上的一点,作于点 , 且满足.下面结论,其中正确的结论是:
A、变小 B、不变 C、变大 D、无法判断12. 如图,点为矩形的边长上的一点,作于点 , 且满足.下面结论,其中正确的结论是:①平分;②为等腰三角形;③;④其中正确的结论有多少个?( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 式子 在实数范围内有意义,则 x 的取值范围是 .14. 如图,为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理 .
 15. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为
15. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为 16. 如图,矩形ABCD中,AB=3,BC=5,过对角线交点O作OE⊥AC交 AD于点E,则AE的长是 .
16. 如图,矩形ABCD中,AB=3,BC=5,过对角线交点O作OE⊥AC交 AD于点E,则AE的长是 .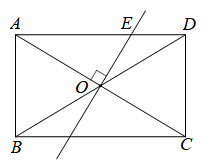 17. 如图,将矩形沿对角线所在直线折叠,点C落在同一平面内,落点记为 , 与交于点E,若 , 则的长为 .
17. 如图,将矩形沿对角线所在直线折叠,点C落在同一平面内,落点记为 , 与交于点E,若 , 则的长为 . 18. 如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于 .
18. 如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于 .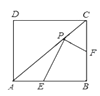
三、解答题
-
19. 已知 = ,求代数式 的值.20. 计算(1)、 ;(2)、 .21. 如图,每个小正方形的边长为1.
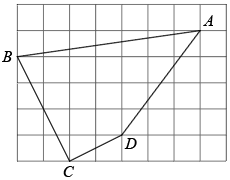 (1)、求四边形的面积和周长;(2)、是直角吗?说明理由.22. 如图,在四边形中, , , , . 求的度数.
(1)、求四边形的面积和周长;(2)、是直角吗?说明理由.22. 如图,在四边形中, , , , . 求的度数. 23. 如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.
23. 如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.
 24. 如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
24. 如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. (1)、求证:四边形ABFE是平行四边形;(2)、若∠BEF=∠DAE,AE=3,BE=4,求EF的长.25. 如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
(1)、求证:四边形ABFE是平行四边形;(2)、若∠BEF=∠DAE,AE=3,BE=4,求EF的长.25. 如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E. (1)、求证:△ADO≌△CBO.(2)、求证:四边形ABCD是菱形.(3)、若DE = AB = 2,求菱形ABCD的面积.26. 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1)、求证:△ADO≌△CBO.(2)、求证:四边形ABCD是菱形.(3)、若DE = AB = 2,求菱形ABCD的面积.26. 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
 (1)、①依题意补全图形;
(1)、①依题意补全图形;②求证:BE⊥AC.
(2)、请探究线段BE,AD,CN所满足的等量关系,并证明你的结论.(3)、设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为(直接写出答案).