湖南省永州市新田县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-04 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在中, , , , 则的度数是( )
2. 如图,在中, , , , 则的度数是( ) A、 B、 C、 D、3. 在中, , 的对边长分别为 , 则下列等式错误的是( )A、 B、 C、 D、4. 如图, , 以点为圆心,以适当长为半径作弧交于点 , 交于点;分别以为圆心,以大于的长为半径作弧,两弧在内部相交于点;画射线 , 在射线上截取线段 , 则点到的距离为( )
A、 B、 C、 D、3. 在中, , 的对边长分别为 , 则下列等式错误的是( )A、 B、 C、 D、4. 如图, , 以点为圆心,以适当长为半径作弧交于点 , 交于点;分别以为圆心,以大于的长为半径作弧,两弧在内部相交于点;画射线 , 在射线上截取线段 , 则点到的距离为( ) A、8 B、6 C、5 D、45. 从一个多边形的一个顶点出发,最多可画条对角线,则它是( )边形.A、 B、 C、 D、6. 如图,在中, , 分别是的中点,则的长是( )
A、8 B、6 C、5 D、45. 从一个多边形的一个顶点出发,最多可画条对角线,则它是( )边形.A、 B、 C、 D、6. 如图,在中, , 分别是的中点,则的长是( ) A、5 B、6 C、7 D、97. 如图,平行四边形的对角线交于点 , 且 , 的周长为19,则的两条对角线的和是( )
A、5 B、6 C、7 D、97. 如图,平行四边形的对角线交于点 , 且 , 的周长为19,则的两条对角线的和是( ) A、12 B、13 C、26 D、248. 如图,菱形的对角线相交于点 , 过点作于点 , 连接 , 若 , 则菱形的面积为( )
A、12 B、13 C、26 D、248. 如图,菱形的对角线相交于点 , 过点作于点 , 连接 , 若 , 则菱形的面积为( ) A、36 B、18 C、24 D、649. 如图,在矩形ABCD中,对角线AC与BD交于点O,∠BAD的平分线交BC于E,若 , 则∠COE=( )
A、36 B、18 C、24 D、649. 如图,在矩形ABCD中,对角线AC与BD交于点O,∠BAD的平分线交BC于E,若 , 则∠COE=( ) A、45 B、60 C、75 D、3010. 如图,在正方形中,点分别在上, , 与相交于点 . 下列结论:①垂直平分;②当时,为等边三角形;③当时,;④当时, . 其中正确的结论有( )个.
A、45 B、60 C、75 D、3010. 如图,在正方形中,点分别在上, , 与相交于点 . 下列结论:①垂直平分;②当时,为等边三角形;③当时,;④当时, . 其中正确的结论有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
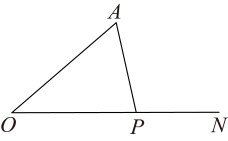
11. 若一个n边形的外角和与它的内角和之和为1800°,则边数n=.12. 如图,已知 , 点是射线上一动点,当为直角三角形时, .
 13. 如图,在中, , 的角平分线交于点 , , 则的周长等于 .
13. 如图,在中, , 的角平分线交于点 , , 则的周长等于 . 14. 如图,已知▱ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 .
14. 如图,已知▱ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 . 15. 如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
15. 如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 . 16. 如图,∠C=90°,AC= , BC=8,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= , △ABC与△APQ全等.
16. 如图,∠C=90°,AC= , BC=8,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= , △ABC与△APQ全等. 17. 如图,在矩形中, , O为对角线的中点,点P在边上,且 , 点Q在边上,连接与 , 则的最大值为 , 的最小值为 .
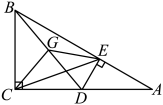
17. 如图,在矩形中, , O为对角线的中点,点P在边上,且 , 点Q在边上,连接与 , 则的最大值为 , 的最小值为 .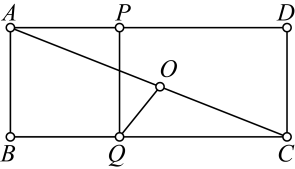 18. 欧几里得古希腊著名数学家、欧氏几何学开创者.下面问题是欧几里得证明勾股定理的证法一小片段!如图,分别以的三边为边长,向外作正方形 .
18. 欧几里得古希腊著名数学家、欧氏几何学开创者.下面问题是欧几里得证明勾股定理的证法一小片段!如图,分别以的三边为边长,向外作正方形 . (1)、连接 , 则(填或);(2)、过点作的垂线,交于点 , 交于点 , 若 , 则正方形的面积是 .
(1)、连接 , 则(填或);(2)、过点作的垂线,交于点 , 交于点 , 若 , 则正方形的面积是 .三、解答题
-
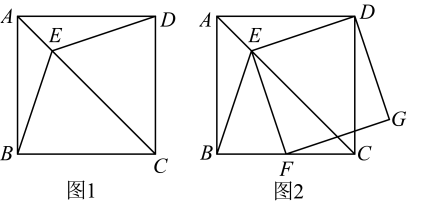
19. 正方形的花坛内准备种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案,下面是三种不同设计方案中的一部分,请把图1、图2补成既是轴对称图形,又是中心对称图形,并画出一条对称轴,把图3补成只是中心对称图形,并把对称中心标上字母 . (在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.)
 20. 如图,在△ABC中,BD⊥AC , AB=20,BC=15,CD=9.
20. 如图,在△ABC中,BD⊥AC , AB=20,BC=15,CD=9. (1)、求AC的长;(2)、判断△ABC的形状并证明.21. 如图,在平行四边形中,点是边的中点,连接并延长,交延长线于点 , 连接 .
(1)、求AC的长;(2)、判断△ABC的形状并证明.21. 如图,在平行四边形中,点是边的中点,连接并延长,交延长线于点 , 连接 . (1)、求证:四边形是平行四边形;(2)、若 , 则当时,四边形是矩形(不用证明)22. 已知:如图,在中,于点为上一点,且 .
(1)、求证:四边形是平行四边形;(2)、若 , 则当时,四边形是矩形(不用证明)22. 已知:如图,在中,于点为上一点,且 . (1)、求证:;(2)、已知 , 求的长.23. 如图,矩形的一条对角线长 , 两条对角线的一个交角 , 求这个矩形的周长和面积.
(1)、求证:;(2)、已知 , 求的长.23. 如图,矩形的一条对角线长 , 两条对角线的一个交角 , 求这个矩形的周长和面积. 24. 如图,在四边形中,为一条对角线, , 为的中点,连接 .
24. 如图,在四边形中,为一条对角线, , 为的中点,连接 . (1)、求证:四边形为菱形;(2)、连接 , 若平分 , , 求的长.
(1)、求证:四边形为菱形;(2)、连接 , 若平分 , , 求的长.