湖南省长沙市明德教育集团2022-2023学年八年级期下学期数学期中考试试卷
试卷更新日期:2023-07-04 类型:期中考试
一、单选题
-
1. 化简的结果是( )A、 B、 C、 D、2. 下列能构成直角三角形的三边长是( )A、 , , B、 , , C、 , , D、 , ,3. 下列各式计算正确的是( )A、 B、 C、 D、4. 矩形具有而菱形不具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、两组对角分别相等5. 如图,公路 , 互相垂直,公路的中点与点被湖隔开,若测得的长为 , 则、两点间的距离为( )
 A、 B、 C、 D、6. 如图,中,平分 , , 则等于( )
A、 B、 C、 D、6. 如图,中,平分 , , 则等于( ) A、 B、 C、 D、7. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、 , B、AB=CD,AD=BC C、OA=OC,OB=OD D、 , AD=BC8. 如图,明德中学数学兴趣小组为测量学校与河对岸的科技馆之间的距离,在的同岸选取点 , 测得 , , , 据此可求得 , 之间的距离为( )
A、 B、 C、 D、7. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、 , B、AB=CD,AD=BC C、OA=OC,OB=OD D、 , AD=BC8. 如图,明德中学数学兴趣小组为测量学校与河对岸的科技馆之间的距离,在的同岸选取点 , 测得 , , , 据此可求得 , 之间的距离为( ) A、 B、 C、 D、9. 已知正比例函数的函数值y随x的增大而增大,则一次函数的图象大致是( )A、
A、 B、 C、 D、9. 已知正比例函数的函数值y随x的增大而增大,则一次函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A、
10. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A、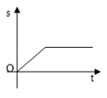 B、
B、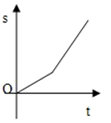 C、
C、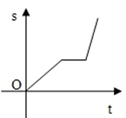 D、
D、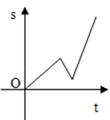
二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是.12. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 .
 13. 一次函数的图象与轴的交点坐标是 .14. 将一次函数y=2x-1的图象向上平移2个单位后所得图象的解析式为 .15. 如图,有两棵树,一棵高米,另一棵高米,两树相距米一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行米
13. 一次函数的图象与轴的交点坐标是 .14. 将一次函数y=2x-1的图象向上平移2个单位后所得图象的解析式为 .15. 如图,有两棵树,一棵高米,另一棵高米,两树相距米一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行米 16. 如图,直线与轴、轴分别交于、两点,是的中点,是上一点,四边形是菱形,其中点坐标为 , , 则的面积为 .
16. 如图,直线与轴、轴分别交于、两点,是的中点,是上一点,四边形是菱形,其中点坐标为 , , 则的面积为 .
三、解答题
-
17. 计算: .18. 如图,在中,∠ACB=90°, , , 于D.
 (1)、求斜边AB的长;(2)、求高CD的长.19. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在 中, ,求 的长.
(1)、求斜边AB的长;(2)、求高CD的长.19. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在 中, ,求 的长. 20. 已知关于的函数 .(1)、若函数为正比例函数,求的值;(2)、若点在函数图象上,求的值;(3)、若随的增大而减小,求的取值范围.21. 如图,已知点、为▱对角线上两点,且 , 连接 , 求证:
20. 已知关于的函数 .(1)、若函数为正比例函数,求的值;(2)、若点在函数图象上,求的值;(3)、若随的增大而减小,求的取值范围.21. 如图,已知点、为▱对角线上两点,且 , 连接 , 求证: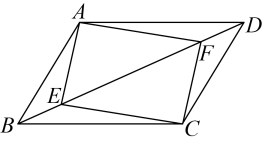 (1)、;(2)、四边形为平行四边形.22. 如图,直线经过点 , 与直线:交于点 .
(1)、;(2)、四边形为平行四边形.22. 如图,直线经过点 , 与直线:交于点 . (1)、求的值和直线的解析式;(2)、直线与轴交于点 , 求的面积;(3)、在轴上是否存在点 , 使得的值最小,若存在,请求出的最小值,若不存在,请说明理由.23. 如图,菱形的对角线 , 相交于点O,点E为菱形外一点,连接、 , 且 , .
(1)、求的值和直线的解析式;(2)、直线与轴交于点 , 求的面积;(3)、在轴上是否存在点 , 使得的值最小,若存在,请求出的最小值,若不存在,请说明理由.23. 如图,菱形的对角线 , 相交于点O,点E为菱形外一点,连接、 , 且 , . (1)、求证:四边形为矩形;(2)、若菱形的边长为4, , 求的面积.24. 我们定义:对角线互相垂直且相等的四边形叫做“神奇四边形”.
(1)、求证:四边形为矩形;(2)、若菱形的边长为4, , 求的面积.24. 我们定义:对角线互相垂直且相等的四边形叫做“神奇四边形”. (1)、在我们学过的下列四边形①平行四边形;②矩形;③菱形;④正方形中,是“神奇四边形”的是(填序号);(2)、如图 , 在正方形中,为上一点,连接 , 过点作于点 , 交于点 , 连、 .
(1)、在我们学过的下列四边形①平行四边形;②矩形;③菱形;④正方形中,是“神奇四边形”的是(填序号);(2)、如图 , 在正方形中,为上一点,连接 , 过点作于点 , 交于点 , 连、 .①求证:四边形是“神奇四边形”;
②如图 , 点、、、分别是、、、的中点试判断四边形是不是“神奇四边形”;
(3)、如图 , 点、分别在正方形的边、上,把正方形沿直线翻折,使得的对应边恰好经过点 , 过点作于点 , 若 , 正方形的边长为 , 求线段的长.25. 已知:在平面直角坐标系中,直线:与轴、轴分别交于、两点,直线经过点 , 与轴交于点 . (1)、求直线的解析式;(2)、如图 , 点为直线上的一个动点,若的面积等于时,请求出点的坐标;(3)、如图 , 将沿着轴平移,平移过程中的记为请问在平面内是否存在点 , 使得以、、、为顶点的四边形是菱形?若存在,直接写出点的坐标.
(1)、求直线的解析式;(2)、如图 , 点为直线上的一个动点,若的面积等于时,请求出点的坐标;(3)、如图 , 将沿着轴平移,平移过程中的记为请问在平面内是否存在点 , 使得以、、、为顶点的四边形是菱形?若存在,直接写出点的坐标.