湖南省湘潭市2023年中考数学试卷
试卷更新日期:2023-07-04 类型:中考真卷
一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的4个选项中,只有一项符合题目要求)
-
1. 中国的汉字既象形又表意,不但其形美观,而且寓意深刻,观察下列汉字,其中是轴对称图形的是( )A、爱 B、我 C、中 D、华2. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥13. 下列计算正确的是( )A、 B、 C、 D、4. 某校组织青年教师教学竞赛活动,包含教学设计和现场教学展示两个方面.其中教学设计占 , 现场展示占 . 某参赛教师的教学设计分,现场展示分,则她的最后得分为( )A、分 B、分 C、分 D、分5. 如图,菱形中,连接 , 若 , 则的度数为( )
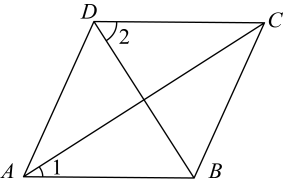 A、 B、 C、 D、6. 如图,平面直角坐标系中,O是坐标原点,点A是反比例函数图像上的一点,过点A分别作轴于点M,轴于直N,若四边形的面积为2.则k的值是( )
A、 B、 C、 D、6. 如图,平面直角坐标系中,O是坐标原点,点A是反比例函数图像上的一点,过点A分别作轴于点M,轴于直N,若四边形的面积为2.则k的值是( )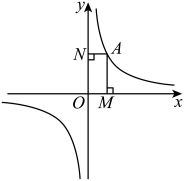 A、2 B、 C、1 D、7. 如图,圆锥底面圆的半径为4,则这个圆锥的侧面展开图中的长为( )
A、2 B、 C、1 D、7. 如图,圆锥底面圆的半径为4,则这个圆锥的侧面展开图中的长为( ) A、 B、 C、 D、8. 某校组织九年级学生赴韶山开展研学活动,已知学校离韶山50千米,师生乘大巴车前往,某老师因有事情,推迟了10分钟出发,自驾小车以大巴车速度的倍前往,结果同时到达.设大巴车的平均速度为x千米/时,则可列方程为( )A、 B、 C、 D、
A、 B、 C、 D、8. 某校组织九年级学生赴韶山开展研学活动,已知学校离韶山50千米,师生乘大巴车前往,某老师因有事情,推迟了10分钟出发,自驾小车以大巴车速度的倍前往,结果同时到达.设大巴车的平均速度为x千米/时,则可列方程为( )A、 B、 C、 D、二、选择题(本题共4小题,每小题3分 ,共12分.在每小题给出的4个选项中,有多项符合题目要求)
-
9. 下列选项中正确的是( )A、 B、 C、 D、10. 2023年湘潭中考体育考查了投掷实心球的项目,为了解某校九年级男生投掷实心球水平.随机抽取了若干名男生的成绩(单位:米),列出了如下所示的频数分布表并绘制了扇形图:
类别
A
B
C
D
E
成绩
频数
2
6
25
12
5
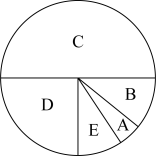
则下列说法正确的是( )
A、样本容量为50 B、成绩在米的人数最多 C、扇形图中C类对应的圆心角为 D、成绩在米的频率为0.111. 如图,是的直径,为弦,过点的切线与延长线相交于点 , 若 , 则下列说法错误的是( )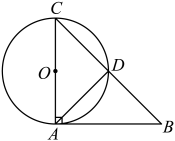 A、 B、 C、 D、12. 如图,抛物线与x轴交于点 , 则下列结论中正确的是( )
A、 B、 C、 D、12. 如图,抛物线与x轴交于点 , 则下列结论中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
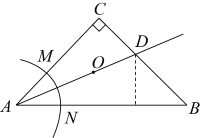
13. 数轴上到原点的距离小于的点所表示的整数有 . (写出一个即可)14. 已知实数a,b满足 , 则 .15. 如图,在中, , 按以下步骤作图:①以点为圆心,以小于长为半径作弧,分别交于点 , ;②分别以 , 为圆心,以大于的长为半径作弧,在内两弧交于点;③作射线 , 交于点 . 若点到的距离为 , 则的长为 .
 16. 七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
16. 七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
四、解答题(本大题共10个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
17. 解不等式组: , 并把它的解集在数轴上表示出来.
 18. 先化简,再求值: , 其中 .19. 在中,是斜边上的高.
18. 先化简,再求值: , 其中 .19. 在中,是斜边上的高.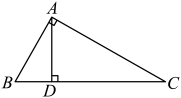 (1)、证明:;(2)、若 , 求的长.20. 为落实“双减”政策要求,丰富学生课余生活,某校七年级根据学生需求,组建了四个社团供学生选择:A(合唱社团)、B(硬笔书法社团)、C(街舞社团)、D(面点社团).学生从中任意选择两个社团参加活动.(1)、小明对这4个社团都很感兴趣,如果他随机选择两个社团,请列举出所有的可能结果;(2)、小宇和小江在选择过程中,首先都选了社团C(街舞社团),第二个社团他俩决定随机选择,请用列表法或树状图求他俩选到相同社团的概率.21. 教育部正式印发《义务教育劳动课程标准(2022年版)》,劳动课成为中小学的一门独立课程,湘潭市中小学已经将劳动教育融入学生的日常学习和生活中某校倡导同学们从帮助父母做一些力所能及的家务做起,培养劳动意识,提高劳动技能.小明随机调查了该校10名学生某周在家做家务的总时间,并对数据进行统计分析,过程如下:
(1)、证明:;(2)、若 , 求的长.20. 为落实“双减”政策要求,丰富学生课余生活,某校七年级根据学生需求,组建了四个社团供学生选择:A(合唱社团)、B(硬笔书法社团)、C(街舞社团)、D(面点社团).学生从中任意选择两个社团参加活动.(1)、小明对这4个社团都很感兴趣,如果他随机选择两个社团,请列举出所有的可能结果;(2)、小宇和小江在选择过程中,首先都选了社团C(街舞社团),第二个社团他俩决定随机选择,请用列表法或树状图求他俩选到相同社团的概率.21. 教育部正式印发《义务教育劳动课程标准(2022年版)》,劳动课成为中小学的一门独立课程,湘潭市中小学已经将劳动教育融入学生的日常学习和生活中某校倡导同学们从帮助父母做一些力所能及的家务做起,培养劳动意识,提高劳动技能.小明随机调查了该校10名学生某周在家做家务的总时间,并对数据进行统计分析,过程如下:收集数据:在家做家务时间:(单位:小时)
1 5 4 1 a 3 2 b 3 4
整理数据:
时间段
人数
3
6
m
分析数据:
统计量
平均数
中位数
众数
数据
3.4
3.5
4
 请结合以上信息回答下列问题:(1)、 , 并补全频数直方图;(2)、数据统计完成后,小明发现有两个数据不小心丢失了.请根据图表信息找回这两个数据.若 , 则 , ;(3)、根据调查结果,请估计该校2000名学生在这一周劳动时间不少于3小时的人数.22. 我国航天事业发展迅速,2023年5月30日9时31分,神舟十六号载人飞船成功发射,某玩具店抓住商机,先购进了1000件相关航天模型玩具进行试销,进价为50元/件.(1)、设每件玩具售价为x元,全部售完的利润为y元.求利润y(元)关于售价x(元/件)的函数表达式;(2)、当售价定为60元/件时,该玩具销售火爆,该店继续购进一批该种航天模型玩具,并从中拿出这两批玩具销售利润的20%用于支持某航模兴趣组开展活动,在成功销售完毕后,资助经费恰好10000元,请问该商店继续购进了多少件航天模型玩具?23. 如图,点A的坐标是 , 点B的坐标是 , 点C为中点,将绕着点B逆时针旋转得到 .
请结合以上信息回答下列问题:(1)、 , 并补全频数直方图;(2)、数据统计完成后,小明发现有两个数据不小心丢失了.请根据图表信息找回这两个数据.若 , 则 , ;(3)、根据调查结果,请估计该校2000名学生在这一周劳动时间不少于3小时的人数.22. 我国航天事业发展迅速,2023年5月30日9时31分,神舟十六号载人飞船成功发射,某玩具店抓住商机,先购进了1000件相关航天模型玩具进行试销,进价为50元/件.(1)、设每件玩具售价为x元,全部售完的利润为y元.求利润y(元)关于售价x(元/件)的函数表达式;(2)、当售价定为60元/件时,该玩具销售火爆,该店继续购进一批该种航天模型玩具,并从中拿出这两批玩具销售利润的20%用于支持某航模兴趣组开展活动,在成功销售完毕后,资助经费恰好10000元,请问该商店继续购进了多少件航天模型玩具?23. 如图,点A的坐标是 , 点B的坐标是 , 点C为中点,将绕着点B逆时针旋转得到 . (1)、反比例函数的图像经过点 , 求该反比例函数的表达式;(2)、一次函数图象经过A、两点,求该一次函数的表达式.24. 问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
(1)、反比例函数的图像经过点 , 求该反比例函数的表达式;(2)、一次函数图象经过A、两点,求该一次函数的表达式.24. 问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.问题设置:把筒车抽象为一个半径为r的 . 如图②,始终垂直于水平面,设筒车半径为2米.当时,某盛水筒恰好位于水面A处,此时 , 经过95秒后该盛水筒运动到点B处.(参考数据,)


问题解决:
(1)、求该盛水筒从A处逆时针旋转到B处时,的度数;(2)、求该盛水筒旋转至B处时,它到水面的距离.(结果精确到米)25. 问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形的边上任意取一点G,以为边长向外作正方形 , 将正方形绕点B顺时针旋转. (1)、特例感知:
(1)、特例感知:当在上时,连接相交于点P,小红发现点P恰为的中点,如图①.针对小红发现的结论,请给出证明;
(2)、小红继续连接 , 并延长与相交,发现交点恰好也是中点P,如图②,根据小红发现的结论,请判断的形状,并说明理由;(3)、规律探究:如图③,将正方形绕点B顺时针旋转 , 连接 , 点P是中点,连接 , , , 的形状是否发生改变?请说明理由.
26. 如图,二次函数的图象与轴交于 , 两点,与轴交于点,其中 , .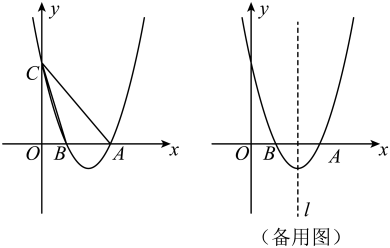 (1)、求这个二次函数的表达式;(2)、在二次函数图象上是否存在点 , 使得?若存在,请求出点坐标;若不存在,请说明理由;(3)、点是对称轴上一点,且点的纵坐标为 , 当是锐角三角形时,求的取值范围.
(1)、求这个二次函数的表达式;(2)、在二次函数图象上是否存在点 , 使得?若存在,请求出点坐标;若不存在,请说明理由;(3)、点是对称轴上一点,且点的纵坐标为 , 当是锐角三角形时,求的取值范围.