浙江省绍兴市诸暨市2022-2023学年七年级下学期期末考试数学试卷

试卷更新日期：2023-07-04 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. 如图，两只手的食指和拇指在同一平面内，在以下四种摆放方式中，它们构成的一对角可以看成内错角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，最适合采用全面调查的是（）

A、对全国中学生身高和体重情况的调查 B、对某厂生产的鞋底能承受的弯折次数的调查 C、调查某水库中现有鱼的数量 D、某班级所有学生的体育成绩

查看试题解析
3. 已知方程 $3 x + y = 10$ ，用关于 $x$ 的代数式表示 $y$ ，正确的是（）

A、 $y = 10 + 3 x$ B、 $y = 10 - 3 x$ C、 $y = - 10 - 3 x$ D、 $y = - 10 + 3 x$

查看试题解析
4. 下列计算正确的是（）

A、 $(2 b)^{3} = 8 b^{3}$ B、 ${(1 0^{7})}^{3} = 1 0^{10}$ C、 $7^{8} \times 7^{3} = 7^{24}$ D、 $(5)^{- 1} = 5$

查看试题解析
5. 下列多项式的变形中，正确的是（）

A、 $y - x = - (x - y)$ B、 $- x - y = - (x - y)$ C、 $- x + y = - (x + y)$ D、 $y + x = - (x + y)$

查看试题解析
6. 下列各等式从左边到右边的变形中，是因式分解的是（）

A、 $(3 - x) (3 + x) = 9 - x^{2}$ B、 $8 x = 2 \times 4 x$ C、 $x^{2} + 4 x + 4 = (x + 2)^{2}$ D、 $x^{2} - 2 x + 1 = x (x - 2) + 1$

查看试题解析
7. 下列多项式的乘法中，可以用平方差公式计算的是（）

A、 $(a + 2 b) (2 a - b)$ B、 $(a + 2 b) (b - 2 a)$ C、 $(b + 2 a) (2 a - b)$ D、 $(b + 2 a) (a - 2 b)$

查看试题解析
8. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{u} + \frac{1}{v} (v \neq f)$ 表示，其中 $f$ 表示照相机镜头的焦距， $u$ 表示物体到镜头的距离， $v$ 表示胶片(像)到镜头的距离.已知 $f$ ， $v$ ，则 $u =$ （）

A、 $\frac{f v}{f - v}$ B、 $\frac{f v}{v - f}$ C、 $\frac{f - v}{f v}$ D、 $\frac{v - f}{f v}$

查看试题解析
9. 设“●，▲，■”分别表示三种不同的物体，如图所示，前面两架天平保持平衡，如果要使第三架也平衡，那么“？”处可以放的物体为（）

A、 B、 C、 D、

查看试题解析
10. 如图，下列选项中：① $∠ 1 = ∠ 2$ ；② $∠ 1 = ∠ 3$ ；③ $∠ 1 = ∠ 4$ ；④ $∠ 2 = ∠ 3$ ；⑤ $∠ 2 = ∠ 4$ ；⑥ $∠ 3 = ∠ 4$ ，单个选项条件可以说明 $E F / / G H$ 的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题(本题有10小题，每小题3分，共30分)

11. 计算： ${(- \frac{1}{2023})}^{0} =$ .

查看试题解析
12. 分解因式： $x^{2} - x$ =.

查看试题解析
13. 已知长方形的周长是 $34 c m$ ，设长方形的长为 $a (c m)$ ，宽为 $b (c m)$ ，则可列方程.

查看试题解析
14. 计算： $- 2 (a - b + c) =$ .

查看试题解析
15. 如图，把长方形ABCD沿着射线AC平移一段距离，则图中标识的线段中，与 $B B^{^{'}}$ 平行且相等的线段（不包括 $B B^{^{'}}$ ）有条.

查看试题解析
16. 某新能源车销售网点第七月至第十二月的销售数量如图所示，则第四季度比第三季度的销售量增加了辆.

查看试题解析
17. 计算： $\frac{a + 3 b}{a + b} + \frac{a - b}{a + b} =$ .

查看试题解析
18. 化简： $(x + 2)^{2} - (x + 2) (x - 2) =$ .

查看试题解析
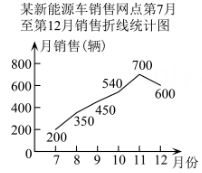19. 如图，六块纸板拼成一张大矩形纸板，其中一块是边长为 $a$ 的正方形，两块是边长为 $b$ 的正方形，三块是长为 $a$ ，宽为 $b$ 的矩形 $(a > b)$ .观察图形，发现多项式 $a^{2} + 3 a b + 2 b^{2}$ 可因式分解为.

查看试题解析

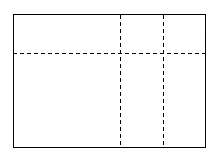20. 现有甲，乙，丙三种糖混合而成的什锦糖50千克，其中各种糖的千克数和单价如下表.

	甲种糖	乙种糖	丙种糖
千克数	20	10	20
单价（元/千克）	15	20	25

商店以糖的平均价（平均价=混合糖的总价格÷混合糖的总千克数）作为什锦糖的单价，要使什锦糖的单价每千克提高1元，则需再加入丙种糖千克.

查看试题解析

三、解答题(本大题共6小题，第21~25题每题6分，第26题10分，共计40分；解答需写出必要的文字说明，演算步骤或证明过程.)

21. 解方程（或方程组）：

(1)、解方程组 ${\begin{array}{l} 2 x + y = 5 \\ x - y = 1 \end{array}$ ；

(2)、解分式方程： $\frac{x + 3}{2 x - 3} = 2$ .

查看试题解析
22. 统计某天7：00~9：00段经过高速公路某测速点的汽车的速度(测得的速度为整数，单位km/h)，得到如下频数直方图和扇形统计图.请回答下列问题：

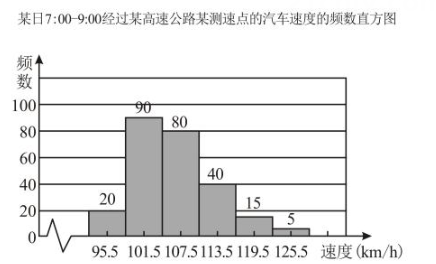(1)、这一天7：00~9：00经过观察点的车辆总数是多少?

(2)、若该路段汽车限速为110km/h(≤110km/h)，问超速行驶的汽车占总数的百分之几?

查看试题解析
23. 先化简，再求值： $\frac{4}{a^{2} - 4} + \frac{1}{a + 2}$ ，其中 $a = - 3$ .

查看试题解析
24. 如图，已知点C，F为直线AB上两点，在AB同侧有三条射线CE，CD，FG，CD平分 $∠ E C B ， C D / / F G$ .

(1)、若 $∠ A C E = 5 0^{°}$ ，求 $∠ B F G$ 的度数.

(2)、若 $∠ A C E = m^{°}$ ，请直接用含 $m$ 的代数式表示 $∠ B F G$ 的度数.

查看试题解析
25. 阅读理解以下材料内容：
完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题.

例：若 $a + b = 3 ， a b = 1$ ，求 $a^{2} + b^{2}$ 的值.

解： $∵ a + b = 3 ， a b = 1 ， ∴ (a + b)^{2} = 9 ， 2 a b = 2$ .

$∴ (a + b)^{2} = a^{2} + 2 a b + b^{2} = 9 . ∴ a^{2} + b^{2} = 7$ .

根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 4 ， x^{2} + y^{2} = 10$ ，求xy的值；应用以上知识进行思维拓展；

(2)、如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，若 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积.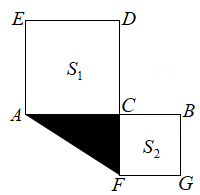

查看试题解析

26. 某工厂需制作如图所示的竖式与横式两种无盖纸盒(单位cm).

情境	内容	图形
情境1	工厂仓库内现存有35cm×35cm的正方形纸板200张，35cm×50cm的长方形纸板400张，用库存纸板制作两种无盖纸盒.
情境2	库存纸板已用完，采购部重新采购了如图规格的纸板，甲纸板尺寸为50cm×70cm，乙纸板尺寸为35cm×85cm，丙纸板尺寸为35cm×70cm.采购甲纸板有800张，乙纸板有400张，丙纸板有300张．纸板裁剪后可制作两种无盖纸盒.
情境3	某次采购订单中，甲种纸板的采购数量为500张，乙种300张，因采购单被墨水污染，导致丙种纸板的具体数字已经模糊不清，只知道百位和十位数字分别为2和4.

根据以上信息，解决以下问题：

(1)、情境1，问两种纸盒各做多少个，恰好将库存纸板用完?

(2)、情境2，问能否通过做适当数量的竖式和横式无盖纸盒，使得纸板的使用率为100%?请通过计算说明理由.

(3)、情境3，若本次采购的纸板裁剪做成竖式和横式无盖纸盒，并使得纸板的使用率为100%请你能帮助工厂确定丙纸板的张数.

查看试题解析