浙江省台州市黄岩区2022-2023学年七年级下学期期末考试数学试卷
试卷更新日期:2023-07-04 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1. 点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,是一条射线.若 , 则的度数是( )
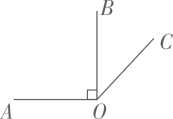 A、 B、 C、 D、3. 一个正方形的面积是13,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 疫情过后,为了解某市600万民众的身体健康状况,从中任意抽取1000人进行调查.在这个问题中,这1000人的身体健康状况是( )A、样本 B、个体 C、总体 D、样本容量5. 若是方程的解,则的值是( )A、-4 B、 C、4 D、166. 两个不等式的解集在数轴上表示如图,则这两个不等式组成的不等式组的解集是( )
A、 B、 C、 D、3. 一个正方形的面积是13,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 疫情过后,为了解某市600万民众的身体健康状况,从中任意抽取1000人进行调查.在这个问题中,这1000人的身体健康状况是( )A、样本 B、个体 C、总体 D、样本容量5. 若是方程的解,则的值是( )A、-4 B、 C、4 D、166. 两个不等式的解集在数轴上表示如图,则这两个不等式组成的不等式组的解集是( ) A、或 B、 C、 D、7. 下列命题中,真命题的是( )A、如果两个角的和等于 , 那么这两个角互为补角 B、内错角相等 C、如果两条直线平行,那么同旁内角相等 D、有三条直线如果 , 那么8. 一次智力测试有20道选择题.该测试题的评分标准是:答对1题得5分,答错1题扣2分,不答题得0分.小明有2道题末答,要使总分不低于60分,答对的题数至少是( )A、12 B、13 C、14 D、159. 用大小完全相同的长方形在直角坐标系中摆成如图所示图案,已知点A的坐标为(-14,6),则点B的坐标是( )
A、或 B、 C、 D、7. 下列命题中,真命题的是( )A、如果两个角的和等于 , 那么这两个角互为补角 B、内错角相等 C、如果两条直线平行,那么同旁内角相等 D、有三条直线如果 , 那么8. 一次智力测试有20道选择题.该测试题的评分标准是:答对1题得5分,答错1题扣2分,不答题得0分.小明有2道题末答,要使总分不低于60分,答对的题数至少是( )A、12 B、13 C、14 D、159. 用大小完全相同的长方形在直角坐标系中摆成如图所示图案,已知点A的坐标为(-14,6),则点B的坐标是( )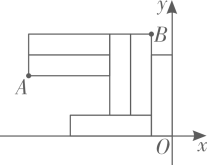 A、 B、 C、 D、10. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A、 B、 C、 D、10. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )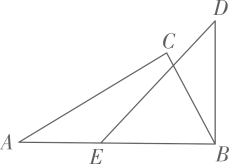 A、或或 B、或或 C、或或 D、或或
A、或或 B、或或 C、或或 D、或或二、填空题(本题有6小题,每小题4分,共24分)
-
11. 的算术平方根为 .
12. 在平面直角坐标系中,点在轴上,且位于原点右侧,距离原点3个单位长度,则点的坐标为.13. 一组数据的最大值与最小值之差为50,若取组距为7,那么这组数据应分成组.14. 如图,在方格内填入了一些表示数的式子,若图中各行、各列及对角线上的三个数之和都相等,则.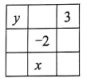 15. 如图,将一条长方形纸带折叠,EF为折痕,CE交BF于点.若的度数是度数的2倍,则的度数为.
15. 如图,将一条长方形纸带折叠,EF为折痕,CE交BF于点.若的度数是度数的2倍,则的度数为. 16. 已知是非负整数,且同时满足 , 则.
16. 已知是非负整数,且同时满足 , 则.三、解答题(本题有8大题,第17,18题每题6分,第 rId125 题每题8分,第23题10分,第24题12分,共66分
-
17. 计算:(1)、;(2)、18. 解方程组:.19. 如图,已知直线EF分别交直线AB,CD于点.求证:.

证明:(已知),
( ).
( ).
即 ▲ = ▲ .
▲ ∥ ▲ ( )
( ).
20. 如图,在平面直角坐标系中,有一个三角形ABC,点A'的坐标是(-2,2),现将三角形ABC平移,使点A变换为点A',点B',C"分别是点B,C的对应点. (1)、请画出平移后的三角形A'B'C'(不写画法),并直接写出点B',C'的坐标;(2)、若三角形ABC内部有一点P,其平移后的对应点为P'(-2,1),则点P的坐标是.21. 随着科技的发展,诈骗形式越来越多样化.近期,我市出现多起人工智能诈骗案件,且涉案金额颇大.为加强学生的安全反诈骗意识,全市组织了学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)、请画出平移后的三角形A'B'C'(不写画法),并直接写出点B',C'的坐标;(2)、若三角形ABC内部有一点P,其平移后的对应点为P'(-2,1),则点P的坐标是.21. 随着科技的发展,诈骗形式越来越多样化.近期,我市出现多起人工智能诈骗案件,且涉案金额颇大.为加强学生的安全反诈骗意识,全市组织了学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题.组别
成绩x/分
频数
A组
60≤x<70
a
B组
70≤x<80
8
C组
80≤x<90
12
D组
90≤x<100
14
 (1)、一共抽取了个参赛学生的成绩,表中=;(2)、补全频数分布直方图;(3)、计算扇形统计图中“B”对应的圆心角度数;(4)、若成绩在80分以上(包括80分)的为“优秀”,请估计我市120万学生在本次竞赛中获得“优秀”的人数.22. 近两年,某市旅游火热出圈.为维护市场价格秩序,市政府对酒店民宿的房源价格涨幅作出规定:基础房源在平时的房价基础上涨幅不超过150%.某酒店有A型和B型两种客房各8间、10间,两种房型每天的标价之和为650元.一个旅游团住了3间A型房间和2间B型房间,一天共花去住宿费1600元.(1)、求A型房和B型房每天的标价;(2)、“五一”期间,该酒店准备将两种房型的标价调高相同的价格,以达到在每天房间全部住满的情况下营业额超过7700元的目标,该酒店的调控价格应控制在什么范围?23. 已知直线 , 垂足为点 , 点A,B分别在直线OA,OB上.点是平面上任一点,连接PA,PB
(1)、一共抽取了个参赛学生的成绩,表中=;(2)、补全频数分布直方图;(3)、计算扇形统计图中“B”对应的圆心角度数;(4)、若成绩在80分以上(包括80分)的为“优秀”,请估计我市120万学生在本次竞赛中获得“优秀”的人数.22. 近两年,某市旅游火热出圈.为维护市场价格秩序,市政府对酒店民宿的房源价格涨幅作出规定:基础房源在平时的房价基础上涨幅不超过150%.某酒店有A型和B型两种客房各8间、10间,两种房型每天的标价之和为650元.一个旅游团住了3间A型房间和2间B型房间,一天共花去住宿费1600元.(1)、求A型房和B型房每天的标价;(2)、“五一”期间,该酒店准备将两种房型的标价调高相同的价格,以达到在每天房间全部住满的情况下营业额超过7700元的目标,该酒店的调控价格应控制在什么范围?23. 已知直线 , 垂足为点 , 点A,B分别在直线OA,OB上.点是平面上任一点,连接PA,PB (1)、当点P在如图1所示位置时, , 则°;(2)、当点移动到如图2所示位置时,求之间的数量关系,并说明理由:(3)、如图3,在(2)的条件下分别作的角平分线交于点 ,
(1)、当点P在如图1所示位置时, , 则°;(2)、当点移动到如图2所示位置时,求之间的数量关系,并说明理由:(3)、如图3,在(2)的条件下分别作的角平分线交于点 ,①若 , 求的度数;
②请直接写出和的数量关系.
24. 定义:已知平面上两点 , 称为A,B两点之间的折线距离.例如点与点之间的折线距离为.如图,已知平面直角坐标系中点. (1)、;(2)、过点作直线平行于轴,求直线上与点的折线距离为5的点的坐标;(3)、已知点 , 且 , 求的取值范围;(4)、已知平面上点与原点的折线距离为3,即 , 直接写出所有满足条件的点围成的图形面积.
(1)、;(2)、过点作直线平行于轴,求直线上与点的折线距离为5的点的坐标;(3)、已知点 , 且 , 求的取值范围;(4)、已知平面上点与原点的折线距离为3,即 , 直接写出所有满足条件的点围成的图形面积.