广东省中山市2022-2023学年七年级下学期期末测试数学试卷

试卷更新日期：2023-07-04 类型：期末考试

进入出卷网下载

一、单项选择题(共10个小题，每小题3分，满分30分)

1. 下列四个数中，属于无理数的是（）

A、0 B、 $\frac{1}{3}$ C、 $π$ D、-1.5

查看试题解析
2. 下列调查中，最适宜采用普查的是（）

A、调查某批次汽车的抗撞击能力 B、调查某河流的水质情况 C、调查一批防疫口罩的质量 D、调查运载火箭零部件的质量

查看试题解析
3. 若 $p > q$ ，则下列选项中成立的是（）

A、 $p + 2 > q + 2$ B、 $p - 2 < q - 2$ C、 $2 p < 2 q$ D、 $- \frac{p}{2} > - \frac{q}{2}$

查看试题解析
4. 如图，直线a，b被直线c所截，则∠1与∠2是（）

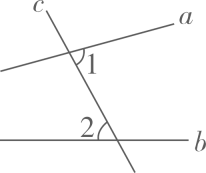A、对顶角 B、同位角 C、同旁内角 D、内错角

查看试题解析
5. 在一个扇形统计图中，某部分所对的圆心角为90°，则该部分占总体的百分比是（）

A、20% B、25% C、30% D、45%

查看试题解析
6. 如图，计划把河水引到A处，应在河岸B(AB⊥l于点B)处挖渠才能使水渠的长度最短，这样做的依据是（）

A、垂线段最短 B、两点之间，线段最短 C、两点确定一条直线 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
7. 在平面直角坐标系中，下列各点在x轴上的是（）

A、(3，3) B、(2，0) C、(0，1) D、(-2，6)

查看试题解析
8. 不等式x-3<0的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 已知m，n满足 ${\begin{array}{l} m + n = - 3 ， \\ m - n = - 1 ， \end{array}$ 则点 $(m ， n)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 若关于 $x$ 的不等式组 ${\begin{array}{l} 2 x + 4 > 0 ， \\ x - k < 1 \end{array}$ 只有3个整数解，则 $k$ 可能是（）

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题(共5个小题，每小题3分，满分15分)

11. 比较大小：3 $\sqrt{7}$ (填写“＞”、“＜”或“=”).

查看试题解析
12. 点 $P (2 ， 4)$ 到 $y$ 轴的距离为.

查看试题解析
13. 在绘制频数分布直方图时，一组数据的最大值与最小值的差为11.若取组距为3，则这组数据应分成组.

查看试题解析
14. 如图，点O在直线AB上， $O C ⊥ O D ， ∠ A O D = 11 0^{°}$ ，则 $∠ B O C =$ °

查看试题解析
15. 如图，在长为 $20 m$ ，宽为 $16 m$ 的长方形空地上，沿平行于各边分割出三个形状、大小一样的小长方形花圃，则其中一个小长方形花圃的长为m.

查看试题解析

三、解答题(一)(共3个小题，每小题8分，满分24分)

16. 计算： $| - \sqrt{2} | + \sqrt{16} + \sqrt[3]{- 27}$ .

查看试题解析
17. 已知 ${\begin{array}{l} x = 2 ， \\ y = a \end{array}$ 是关于 $x ， y$ 的二元一次方程 ${\begin{array}{l} x + y = 3 ， \\ 2 x + y = b \end{array}$ 的解，求 $a + b$ 的值.

查看试题解析
18. 如图， $△ A B C$ 在平面直角坐标系中，其中点 $A (- 3 ， - 2)$ ，点 $B (- 4 ， 1)$ ，点 $C (- 1 ， 3)$ .

(1)、将 $△ A B C$ 向右平移4个单位得到 $△ A_{1} B_{1} C_{1}$ ，在图中画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积.

查看试题解析

四、解答题(二)(共3个小题，每小题9分，满分27分)

19. 为了解七年级学生对垃圾分类相关知识的了解情况，某校对七年级学生进行了垃圾分类相关知识测试，测试成绩全部合格．随机抽取了部分学生的成绩，整理并制作成如下不完整的图表：

分数段	频数	频率
60≤x<70	9	a
70≤x<80	36	0.4
80≤x<90	27	0.3
90≤x≤100	b	0.2

请根据上述统计图表，解答下列问题：

(1)、表中

a =

，

b =

；

(2)、请补全频数分布直方图；

(3)、如果80分以上(含80分)为优秀，根据以上数据，请你估算一下该校七年级800名学生中成绩优秀的人数.

查看试题解析

20. 如图，已知直线AB，CD被直线BC所截，且 $∠ 1 + ∠ 2 = 18 0^{°}$ .

(1)、求证：AB∥CD；

(2)、若 $B D$ 平分 $∠ A B C ， ∠ D = 4 0^{°}$ ，求 $∠ 1$ 的大小.

查看试题解析
21. 某校为丰富学生课余生活，欲购买一批象棋和围棋.已知购买3副象棋和2副围棋共需180元，购买2副象棋和1副围棋共需110元.

(1)、求每副象棋和围棋的价格；

(2)、若学校准备购买象棋和围棋总共30副，且总费用不超过1100元，求最多能购买多少副象棋?

查看试题解析

五、解答题(三)(共2个小题，每小题12分，满分24分)

22. 已知 $△ E F G$ 为直角三角形， $∠ E F G = 9 0^{°}$ ，点 $G$ 在直线AB上.

(1)、如图1，过点 $F$ 作 $C D / / A B$ ，其中 $∠ A G F = 12 6^{°}$ .求 $∠ E F D$ 的大小；

(2)、如图2，过点 $E$ 作 $C D / / A B$ ，求证： $∠ A G F + ∠ C E F = 9 0^{°}$ .

查看试题解析
23. 定义“点P的k阶点”：若点P的坐标为(x，y)，则把坐标为(kx+y，x-ky)的Q点称为点P的k阶点(其中 $k$ 为正整数).例如：点 $P (3 ， 4)$ 的2阶点为点 $Q (2 \times 3 + 4 ， 3 - 2 \times 4)$ 即 $Q (10 ， - 5)$ .

(1)、若点 $P (x ， y)$ 的3阶点为点 $Q (- 1 ， - 7)$ ，求点 $P$ 的坐标；

(2)、若点 $P (t + 1 ， 2 t)$ 的2阶点为点 $Q$ ，将点 $Q$ 先向右移动6个单位，再向下移动3个单位得到点 $Q_{1}$ ，点 $Q_{1}$ 在第一象限，求 $t$ 的取值范围.

查看试题解析