广西防城港市2022-2023学年八年级第二学期期末考试数学试卷

试卷更新日期：2023-07-04 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用 rId5 铅笔把答题卡上对应题目的答案标号涂黑.）

1. $\sqrt{5}$ 的相反数是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $\pm \sqrt{5}$ D、5

查看试题解析
2. 下列图象中，表示 $y$ 是 $x$ 的一次函数的是（）

A、 B、 C、 D、

查看试题解析
3. 一个木匠要制作矩形的踏板，他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次，就能得到矩形的踏板，这样做最直接的道理是（）

A、有两个角是直角的四边形是矩形 B、有三个角是直角的四边形是矩形 C、对角线相等的平行四边形是矩形 D、一组对边平行且相等的四边形是矩形.

查看试题解析
4. 下列各组数是三角形的三边，不能组成直角三角形的一组数是（）

A、 $a = 3 ， b = 4 ， c = 5$ B、 $a = 6 ， b = 8 ， c = 10$ C、 $a = 3 ， b = 5 ， c = 7$ D、 $a = 5 ， b = 12 ， c = 13$

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{3} - \sqrt{2} = 1$ D、 $\sqrt{4} \div \sqrt{2} = 2$

查看试题解析
6. 如图，在直角三角形ABC中， $∠ A C B = 9 0^{°} ， A B = 5 ， D$ 为AB的中点，则CD的长为（）

A、2.5 B、3 C、3.5 D、4

查看试题解析
7. 菱形具有而矩形不一定具有的性质是（）

A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、四条边相等

查看试题解析
8. 某招聘考试分笔试和面试两种，其中笔试按40%、面试按60%计算加权平均数作为总成绩，小华笔试成绩为90分，面试成绩为85分，那么小华的总成绩是（）

A、87分 B、87.5分 C、88分 D、89分

查看试题解析
9. 数据2、3、3、4的方差是（）

A、2 B、1.5 C、0.5 D、0.3

查看试题解析
10. 防城港市科技馆是以“探索·多彩·科技”为展示主题的场馆，是提高我市青少年科学文化素质的重要平台，如图是某天参观科技馆的人数统计图．若高中生有80人，则初中生有（）

A、57人 B、60人 C、70人 D、90人

查看试题解析
11. 已知点 $A (- 1 ， y_{1}) ， B (2 ， y_{2})$ 是一次函数 $y = x - 1$ 图象上的两个点，则 $y_{1} ， y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{2} < y_{1}$ C、 $y_{1} = y_{2}$ D、不能确定

查看试题解析
12. 如图，将矩形ABCD沿直线AE折叠，顶点 $D$ 恰好落在BC边上点 $F$ 处，已知 $C E = 3 c m ， A B = 8 c m$ ，则图中阴影部分的面积为（）

A、20 B、24 C、28 D、30

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分.）

13. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
14. “同位角相等，两直线平行”的逆命题是.

查看试题解析
15. 甲、乙两位同学在近五次数学测试中，平均成绩均为90分，方差分别为 $S_{甲}^{2} = 0.70 ； S_{乙}^{2} = 0.73$ ，甲、乙两位同学成绩较稳定的是同学．

查看试题解析
16. 如图， $□ A B C D$ 的对角线AC、BD相交于点 $O$ ，点 $E$ 是CD的中点，若 $O E = 3$ ，则BC的长为.

查看试题解析
17. 化简： $- \sqrt{{(- \frac{2}{5})}^{2}} =$ .

查看试题解析
18. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为 $a$ ，较短直角边长为 $b$ ，若 $(a + b)^{2} = 21$ ，大正方形的面积为13，则小正方形的面积为.

查看试题解析

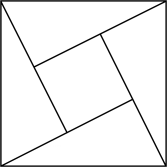
三、解答题（本大题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤.）

19. 计算： $\sqrt{8} - 2 + \sqrt{2} (\sqrt{2} - 1)$ .

查看试题解析
20. 已知 $x = \sqrt{3} + 1 ， y = \sqrt{3} - 1 ，$ 求下列各式的值：

(1)、 $x^{2} + 2 x y + y^{2}$ ；

(2)、 $x^{2} - y^{2}$ .

查看试题解析
21. 【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现：系在旗杆顶端的绳子垂到了地面，并多出了一段，但这条绳子的长度未知.

【实践探究】设计测量方案：

第一步：先测量比旗杆多出的部分绳子的长度，测得多出部分绳子的长度是1米；

第二步：把绳子向外拉直，绳子的底端恰好接触地面的点 $C$ ，再测量绳子底端 $C$ 与旗杆根部 $B$ 点之间的距离，测得距离为5米；

【问题解决】设旗杆的高度AB为 $x$ 米，通过计算即可求得旗杆的高度.

(1)、依题知 $B C =$ 米，用含有 $x$ 的式子表示AC为米；

(2)、请你求出旗杆的高度.

查看试题解析

22. 某学校对八年级甲、乙两班各45名学生进行科普知识测试（满分为60分），测试完成后分别从两个班中各抽取了12份成绩，整理分析过程如下，请补充完整.收集数据：

甲班12名学生测试成绩统计如下：45，59，60，38，57，53，52，58，60，50，43，49

乙班12名学生测试成绩统计如下：35，55，46，39，54，47，43，57，42，59，60，47

整理数据：按如下分数段整理，描述这两组样本数据

组别频数	35≤x＜40	40≤x＜45	45≤x＜50	50≤x＜55	55≤x≤60
甲	1	1	2	3	5
乙	2	2	3	1	4

分析数据：两组样本数据的平均数、众数、中位数如表所示：

班级	平均数	众数	中位数
甲	52	x	52.5
乙	48.7	47	y

(1)、填空：x= ， y=；

(2)、若规定成绩在40分及以上为合格，请估计乙班45名学生本次科普知识测试成绩合格的有多少人？

(3)、你认为哪个班的学生对科普知识掌握的整体水平较好？请说出一个理由.

查看试题解析

23. 如图，平行四边形ABCD的对角线AC，BD相交于点O.E，F是AC上的两个点，并且 $A E = C F$ ，连接DE，BF.

(1)、求证： $△ D O E ≅ △ B O F$

(2)、若 $B D = E F$ ，请在图中连接 $E B ，$ $D F$ ，判断四边形 $E B F D$ 的形状，并证明你的结论.

查看试题解析
24. 如图，一次函数 $y = \frac{1}{2} x + b$ 的图象与 $y$ 轴交于点 $A (0 ， 2)$ ，与 $x$ 轴交于点 $B$ .

(1)、求一次函数的解析式及点 $B$ 的坐标；

(2)、求 $△ A O B$ 的面积；

(3)、直接写出不等式 $\frac{1}{2} x + b > 2$ 的解集.

查看试题解析
25. 如图， $△ A B C$ 中， $∠ A C B = 9 0^{°} ， E F$ 垂直平分BC，垂足为 $D$ ，交AB于点 $F ， C E / / A B$ ，连接BE、CF.

(1)、求证： $C E = B F$ ；

(2)、求证四边形 $C F B E$ 是菱形；

(3)、若AB=10，BC=8，求DF的长.

查看试题解析
26. 如图1，在底面为正方形且高为50cm的长方体的容器底部，放入一个小长方体铁块，现在以均匀的速度往容器中注水，图2是容器内水面高度随时间改变的函数关系图象，观察图中所提供的信息，解答下列问题：

(1)、从开始注水到水面恰好淹没小长方体铁块，共用了分钟，铁块的高为cm；

(2)、求直线AB的函数关系式；

(3)、①求该容器注满水需多少分钟﹖②直接写出长方体铁块的体积与容器的容积之比.

查看试题解析