福建省龙岩市武平县2022-2023学年七年级下学期期末考试数学试卷
试卷更新日期:2023-07-04 类型:期末考试
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
-
1. 下列图形中,由 ,能得到 的是( )A、
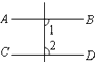 B、
B、 C、
C、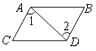 D、
D、 2. 下列实数中,最大的数是( )A、π B、 C、 D、33. 如图,将三角形ABC沿着PQ方向平移得到三角形A'B'C',则下列结论错误的是( )
2. 下列实数中,最大的数是( )A、π B、 C、 D、33. 如图,将三角形ABC沿着PQ方向平移得到三角形A'B'C',则下列结论错误的是( ) A、AB//A'B' B、AA'=BB' C、AA'//BB' D、AA'=AB4. 下列调查中,适合采用抽样调查的是( )A、为保证神舟飞船的顺利飞行,对其零部件进行检查 B、了解一批袋装食品是否含有防护剂 C、全国人口普查 D、企业招聘,对应聘人员进行面试5. 如图所示,点P到直线l的距离是( )
A、AB//A'B' B、AA'=BB' C、AA'//BB' D、AA'=AB4. 下列调查中,适合采用抽样调查的是( )A、为保证神舟飞船的顺利飞行,对其零部件进行检查 B、了解一批袋装食品是否含有防护剂 C、全国人口普查 D、企业招聘,对应聘人员进行面试5. 如图所示,点P到直线l的距离是( )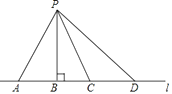 A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度6. 某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x,女生人数为y,则下列方程组中,能正确计算出x、y的是( )A、 B、 C、 D、7. 若 , 则下列结论正确的是( )A、 B、 C、 D、8. 小明家位于公园的正东方向500m处,从小明家出发向北走600m就到小华家.若选取小华家所在位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则公园的坐标是( )A、(-600,-500) B、(500,600) C、(-500,-600) D、(600,500)9. 如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(6,0),把△OAB沿x轴向右平移4个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为12,则图中阴影部分的面积为( )
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度6. 某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x,女生人数为y,则下列方程组中,能正确计算出x、y的是( )A、 B、 C、 D、7. 若 , 则下列结论正确的是( )A、 B、 C、 D、8. 小明家位于公园的正东方向500m处,从小明家出发向北走600m就到小华家.若选取小华家所在位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则公园的坐标是( )A、(-600,-500) B、(500,600) C、(-500,-600) D、(600,500)9. 如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(6,0),把△OAB沿x轴向右平移4个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为12,则图中阴影部分的面积为( ) A、2 B、4 C、6 D、810. 数轴上A、B两点分别表示数a和b,满足3a+b=6-6t,a+2b=3t-3,且AB的长为kt-k,其中t>1,则k的值为( )A、3 B、4 C、5 D、6
A、2 B、4 C、6 D、810. 数轴上A、B两点分别表示数a和b,满足3a+b=6-6t,a+2b=3t-3,且AB的长为kt-k,其中t>1,则k的值为( )A、3 B、4 C、5 D、6二、填空题:本题共6小题,每小题4分,共24分.
-
11. ;.12. 关于x,y的二元一次方程的一个解为 , 则.13. 某校为了解七年级900名学生每周课外阅读情况,随机抽取该年级45名学生进行调查,绘制了如图频数分布直方图.可以估计该年级阅读时间不少于8小时的学生约有人.
 14. 如图,将一张长方形纸片如图所示折叠后,如果∠1=126°,那么∠2等于.
14. 如图,将一张长方形纸片如图所示折叠后,如果∠1=126°,那么∠2等于. 15. 一次数学知识抢答比赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,某同学获得优秀(85分或85分以上),则这位同学至少答对了道题.16. 在平面直角坐标系xOy中,正方形ABCD的顶点A,B的坐标分别为(a,a),(a,a-3),则点C的坐标为.(用含a的式子表示)
15. 一次数学知识抢答比赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,某同学获得优秀(85分或85分以上),则这位同学至少答对了道题.16. 在平面直角坐标系xOy中,正方形ABCD的顶点A,B的坐标分别为(a,a),(a,a-3),则点C的坐标为.(用含a的式子表示)三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.
-
17. 计算18. 解方程组 .19. 解不等式组 .20. 如图,AC∥FE,∠1+∠3=180°.求证:∠FAB=∠4.
 21. 如图,在正方形网格中,A,B两点的坐标分别为(1,3),(2,2).
21. 如图,在正方形网格中,A,B两点的坐标分别为(1,3),(2,2). (1)、写出图中点C的坐标;(2)、将点A向左平移1个单位长度,再向上平移1个单位长度,所得的点为M,直接写出M的坐标并求△BCM的面积.22. 在贯彻落实“五育并举”的工作中,某校在课后服务中开设了多门校本选修课.为了了解全校学生对“客家地方特色美食烹饪”,“中华传统文化美德讲习”,“客家传统节日习俗赏析”和“客家民俗体育项目传承”4门选修课的喜爱情况,随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):
(1)、写出图中点C的坐标;(2)、将点A向左平移1个单位长度,再向上平移1个单位长度,所得的点为M,直接写出M的坐标并求△BCM的面积.22. 在贯彻落实“五育并举”的工作中,某校在课后服务中开设了多门校本选修课.为了了解全校学生对“客家地方特色美食烹饪”,“中华传统文化美德讲习”,“客家传统节日习俗赏析”和“客家民俗体育项目传承”4门选修课的喜爱情况,随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):调查目的
了解××中学学生对4门选修课的喜爱情况
调查方式
抽样调查
调查对象
××中学学生
调查内容
①你的性别是( )
A.男B.女
②下列4门选修课中,你最喜欢的是( )(只能单选)
A 客家地方特色美食烹饪B 中华传统文化美德讲习
C 客家传统节日习俗赏析D 客家民俗体育项目传承
填完后,请将问卷交给数学课代表.
数据的收
集、整理
与描述


调查结论
……
请根据以上调查报告,解答下列问题:
(1)、求参与本次抽样调查的男生人数及选择“客家地方特色美食烹饪”选修课的男生人数;(2)、国家提倡发展体育运动,该学校现有女生1600名,请估计全校女生选择“客家民俗体育项目传承”的人数.23. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具,某汽车4S店计划购进一批新能源汽车进行销售.据了解,购进3辆A型新能源汽车、2辆B型新能源汽车共需95万元;购进4辆A型新能源汽车、1辆B型新能源汽车共需110万元.(1)、问A、B两种型号的新能源汽车每辆进价分别为多少万元?(2)、若该公司计划正好用125万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),销售1辆A型汽车可获利1.2万元,销售1辆B型汽车可获利0.8万元,假如这些新能源汽车全部售出,问该公司共有几种购买方案?最大利润是多少万元?24. 定义:在平面直角坐标系xOy中,若点 , 的横坐标值与纵坐标值的有序实数对,都是方程的解,则称三点共线.(如:点的横坐标与纵坐标的有序实数对为是方程的解.)(1)、已知方程 , 判断A、B、C、D四个点中哪三个点共线?.请写出判断过程.(2)、已知方程 ,①对于任意实数的值该方程总有一个固定的解,请求出固定的解;
②以①的解中值为点的横坐标,值为点的纵坐标,若点 , 与点三点共线,求与的值.
25. 如图,点在射线BE上,点在线段AD上,CD平分 , . (1)、当时,求;(2)、点是线段FD上一点,点是线段CD上一点,连接AC,FP.若CA为的角平分线, , 探究直线CD上是否存在一点 , 使得.
(1)、当时,求;(2)、点是线段FD上一点,点是线段CD上一点,连接AC,FP.若CA为的角平分线, , 探究直线CD上是否存在一点 , 使得.