浙江省宁波市鄞州区2022-2023学年八年级下学期期末考试数学试卷

试卷更新日期：2023-07-04 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 下列是与体育运动有关的图案，其中属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{(- 3)^{2}} = - 3$

查看试题解析
3. 一个多边形的内角和为 $72 0^{°}$ ，则这个多边形的边数为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 某奶茶店提供三种不同容积的杯子：小杯350毫升，中杯500毫升，大杯700毫升.若厂家想了解哪种容积的杯子最畅销，则下列统计量中最有参考意义的是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 关于 $x$ 的方程 $k x^{2} - 4 x + 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值可能是（）

A、0 B、2 C、4 D、6

查看试题解析
6. 若反比例函数 $y = - \frac{6}{x}$ 的图象经过点 $A (a ， b)$ ，则下列结论中不正确的是（）

A、点 $A$ 位于第二或四象限 B、图象一定经过 $(- a ， - b)$ C、在每个象限内， $y$ 随 $x$ 的增大而减小 D、图象一定经过 $(- b ， - a)$

查看试题解析
7. 用反证法证明命题：四边形的外角中至多有3个钝角，第一步应假设（）

A、四边形的外角中没有钝角 B、四边形的外角中有1个钝角 C、四边形的外角中有2个钝角 D、四边形的外角全部都是钝角

查看试题解析
8. 小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（）

A、 $200 {(1 + x)}^{2} = 242$ B、 $200 {(1 - x)}^{2} = 242$ C、 $200 (1 + 2 x) = 242$ D、 $200 (1 - 2 x) = 242$

查看试题解析
9. 如图，在 $□ A B C D$ 中，点E，F分别是AB，CD的中点，点M，N在对角线AC上， $A M = C N$ .则下列说法正确的是（）

A、若 $∠ A M E = 9 0^{°}$ ，则四边形ENFM是矩形 B、若 $M N = 2 A M$ ，则四边形ENFM是矩形 C、若 $M N = M F$ ，则四边形ENFM是矩形 D、若 $M N = A D$ ，则四边形ENFM是矩形

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，分别以AB、AC为边向外作正方形ABDE和AFGC.若想要求出 $△ A C D$ 的面积，则只需知道以下哪个图形的面积（）

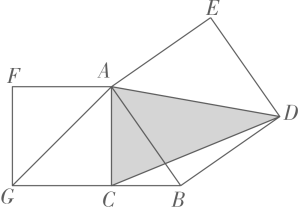A、 $△ A B C$ B、 $△ A B G$ C、正方形ABDE D、四边形AFGB

查看试题解析

二、填空题（每小题3分，共18分）

11. 在二次根式 $\sqrt{x - 1}$ 中，字母 $x$ 的取值范围是.

查看试题解析
12. 在直角坐标系中，若点 $A (1 ， a)$ 和点 $B (b ， 2)$ 关于原点中心对称，则 $a + b =$ .

查看试题解析
13. 小陈参加某单位应聘，计分规则是：笔试的 $60 %$ 和面试的 $40 %$ 作为最终得分，若小陈笔试得90分，面试得80分，则她的最终得分是分.

查看试题解析
14. 已知一元二次方程 $2 x^{2} - 3 x - 1 = 0$ 的两根分别为m、n，则 $\frac{n}{m} + \frac{m}{n}$ 的值为.

查看试题解析
15. 如图，平面直角坐标系中，反比例函数 $y = \frac{2}{x}$ 在第一象限的图象上有一点 $A$ ，过点 $A$ 分别作 $x$ 轴和 $y$ 轴的平行线 $l_{1} ， l_{2}$ .若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象分别与 $l_{1} ， l_{2}$ 交于点 $B ， C ， △ A B C$ 的面积为4，则 $k$ 的值是.

查看试题解析
16. 如图，矩形纸片ABCD中， $A B = 6 ， A D = 8 ， E$ 是AD上一点，将 $△ C D E$ 沿CE对折得到 $△ C F E$ ，延长CF交AB于点 $G$ ，恰有 $G B = G F$ ，则AE的长为.

查看试题解析

三、解答题(第17-19题各6分，第20题7分，第21题8分，第22题9分，第23题10分，共52分)

17. 计算：

(1)、 $\sqrt{12} - \sqrt{3}$ .

(2)、 $(\sqrt{5} + 3 \sqrt{2}) (\sqrt{5} - 3 \sqrt{2})$ .

查看试题解析
18. 解方程：

(1)、 $x^{2} - 4 x - 1 = 0$ .

(2)、 $x (2 x - 1) = 4 x - 2$ .

查看试题解析

19. 某营销店计划从甲、乙两家工厂选择一家进货，要求零件合格的标准尺寸为500mm，现从两家提供的样品中各抽查10件，测得它们的质量如下（单位：mm）.

甲：500，499，500，500，503，498，497，502，500，501；

乙：499，502，498，501，499，501，499，499，500，502.

(1)、为了进一步分析数据，请补全下表中的数据：

种类	平均数	中位数	众数	方差
甲	500	500
乙	500		499	1.8

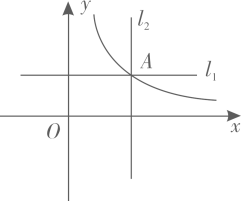
(2)、从零件更符合标准的角度看，你会选择哪一家工厂？说明你的理由.

查看试题解析

20. 在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (- 2 ， 2)$ .

(1)、求反比例函数 $y = \frac{k}{x}$ 表达式；

(2)、已知反比例函数 $y = \frac{k}{x}$ 图象的一支如图所示，补画这个函数图象的另一支；

(3)、在平面直角坐标系中画出 $y = - x$ 的图象，利用图象求不等式 $\frac{k}{x} < - x$ 的解.

查看试题解析
21. 如图，上午9： 00，一轮船在点A处接到警报，台风中心位于轮船正南方向100海里的点B处，轮船以10海里/时的速度由西向东航行，台风中心以20海里/时的速度由南向北移动，距台风中心50海里（包括边界）的圆形区域都属于台风影响区.

(1)、若轮船继续向东航行t小时至A₁ ，此时台风中心位于B₁ ，用含t的代数式表示 $A_{1} {B_{1}}^{2}$ =；

(2)、若轮船不改变航行速度和方向，求轮船开始受台风影响的时刻.

查看试题解析
22. 如图1，在 $△ A B C$ 中，中线BE，CF交于点O，G，H分别是OB，OC的中点，连结EF，FG，GH，HE.

(1)、求证：四边形EFGH是平行四边形；

(2)、如图2，连接OA，若 $O B = 8 ， O C = 6 ， O B ⊥ O C$ ，求四边形BCEF面积和OA的长.

查看试题解析
23. 定义：一组邻边相等，另一组邻边也相等的凸四边形叫做“筝形”.如在凸四边形ABCD中，若 $A B = A D ， B C = D C$ ，则四边形ABCD是“筝形”.

(1)、【新知学习】
如图1，在边长为1的正方形网格中，画出“筝形”ABCD，要求点D是格点；

(2)、【问题探究】
如图2，在矩形ABCD中， $A B = 10 ， B C = 12$ ， “筝形”EFGH的顶点 $E$ 是AB的中点，点F，G，H分别在BC，CD，AD上，且 $E F = 5 \sqrt{2}$ ，求对角线EG的长；

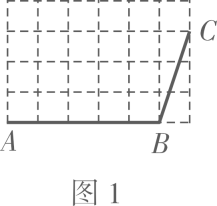
(3)、【拓展思考】
如图3，在“筝形”ABCD中， $A B = A D ， B C = D C = 12 ，$ $∠ B = ∠ D = 9 0^{°} ， E 、 F$ 分别是BC、CD上的点，AE平分 $∠ B E F ， E F ⊥ C D ， E F = 8$ ，求“筝形”ABCD的面积.

查看试题解析