陕西省西安市莲湖区2022-2023学年七年级下册5月月考数学试卷

试卷更新日期：2023-07-04 类型：月考试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列每组数字中，能够成三角形的是（）

A、2、3、5 B、3、3、7 C、13、12、20 D、6、12、6

查看试题解析
2. 下列图形中是轴对称图形的有（）

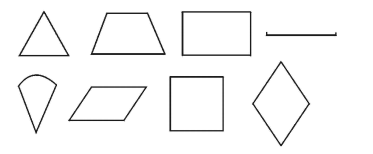A、5 B、6 C、7 D、8

查看试题解析
3. 一个三角形的两边长为2和6，第三边为偶数，则这个三角形的周长为（　　）

A、10 B、12 C、14 D、16

查看试题解析
4. 一定在△ABC内部的线段是（　　）

A、锐角三角形的三条高、三条角平分线、三条中线 B、钝角三角形的三条高、三条中线、一条角平分线 C、任意三角形的一条中线、二条角平分线、三条高 D、直角三角形的三条高、三条角平分线、三条中线

查看试题解析
5. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ， $∠ A C D = 40 °$ ， $∠ B =$ （）

A、40° B、50° C、45° D、60°

查看试题解析
6. 如图，△OAB≌△OCD，若∠A＝80°，OB＝3，则下列说法正确的是（）

A、∠COD＝80° B、CD＝3 C、∠D＝20° D、OD＝3

查看试题解析
7. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块）你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带（）．

A、带①去 B、带②去 C、带③去 D、①②③都带去

查看试题解析
8. 如图，已知A，D，B，E在同一条直线上，且 $A D = B E$ ， $A C = D F$ ，补充下列其中一个条件后，不一定能得到 $△ A B C ≌ △ D E F$ 的是（）

A、 $B C = E F$ B、 $A C ∥ D F$ C、 $∠ C = ∠ F$ D、 $∠ B A C = ∠ E D F$

查看试题解析
9. 如图，把一张长方形的纸按图那样折叠后，B，D两点落在 $B^{'}$ ， $D^{'}$ 点处，若得 $∠ A O B^{'} = 70 °$ ，则 $∠ O G C$ 的度数为（）．

A、55° B、35° C、70° D、60°

查看试题解析
10. 根据下列已知条件，能作出唯一△ABC的是（）

A、AB＝3，BC＝4，CA＝8 B、AB＝4，BC＝3，∠A＝60° C、∠A＝60°，∠B＝45°，AB＝4 D、∠C＝90°，∠B＝30°，∠A＝60°

查看试题解析

二、填空题（每题3分，共18分）

11. 一个三角形的三个内角的度数的比是2：2：1，这个三角形是三角形．

查看试题解析
12. 已知等腰三角形的一个角为75°，则其顶角为．

查看试题解析
13. 如图，已知线段AB与CD相交于点E， $A C = A D$ ， $C E = E D$ ，则图中全等三角形有对．

查看试题解析
14. 如图，在 $△ A B C$ 中，已知点D、点E分别为BC、AD的中点，且 $△ B D E$ 的面积为3，则 $△ A B C$ 的面积是．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ， $∠ A C B = 50 °$ ， BD平分 $∠ A B C$ ， CD平分 $∠ A C B$ ．求 $∠ D$ 的度数为．

查看试题解析
16. 如图，已知等边 $△ A B C$ 和等边 $△ B P E$ ，点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：① $A P = C E$ ；② $∠ P M E = 60 °$ ；③BM平分 $∠ A M E$ ；④ $A M + M C = B M$ ，其中正确的有（填序号）．

查看试题解析

三、解答题(共52分）

17. 尺规作图：
已知： $∠ a$ ，线段a．利用尺规作图求作 $△ A B C$ ，使 $∠ A = a$ ， $A B = a$ ， $A C = 2 a$ ；要求：不写作法，保留作图痕迹，标明字母．

查看试题解析
18. 在 $4 \times 4$ 的正方形网格中，已将图中的四个小正方形涂上阴影（如图），若再从其余小正方形中任选一个也涂上阴影，使得整个阴影部分组成的图形成轴对称图形，画出符合条件的小正方形（最少两种）．

查看试题解析
19. 已知：如下图 $A B ∥ C D$ ， $A B = C D$ ．

求证： $△ A D C ≌ △ C B A$ ．

证明；

查看试题解析
20. 如图，为了测量点B到河对面的目标A之间的距离，在点B同侧选择了一点C，测得 $∠ A B C = 75 °$ ， $∠ A C B = 35 °$ ．然后在点M处立了标杆，使 $∠ C B M = 75 °$ ， $∠ M C B = 35 °$ ，得到 $△ M B C ≌ △ A B C$ ，测得MB的长就是AB的距离．请说明这样做的理由是．

查看试题解析
21. 如图，在 $△$ ABC中AD、AE、AF分别为△ABC的高、角平分线和中线，已知 $△$ AFC的面积为10，AD＝4，∠DAE＝20°，∠C＝30°．

(1)、求BC的长度；

(2)、求∠B的度数．

查看试题解析
22. 如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．

(1)、求证：AE＝CD；

(2)、若AC＝12cm，求BD的长．

查看试题解析
23. 在直角三角形ABC中， $∠ A C B = 90 °$ ，直线l过点C．

(1)、当 $A C = B C$ 时，
①如图1，分别过点A和B作 $A D ⊥$ 直线l于点D， $B E ⊥$ 直线l于点E．求证： $△ A C D ≌ △ C B E$ ；
②如图2，过点A作 $A D ⊥$ 直线l于点D，点B与点F关于直线l对称，连接BF交直线l于E，连接CF．求证： $D E = A D + E F$ ．

(2)、当 $A C = 8 c m$ ， $B C = 6 c m$ 时，如图3，点B与点F关于直线l对称，连接BF、CF．点M从A点出发，以每秒1cm的速度沿 $A \to C$ 路径运动，终点为C，点N以每秒3cm的速度沿 $F \to C \to B \to C \to F$ 路径运动，终点为F，分别过点M、N作 $M D ⊥$ 直线l于点D， $N E ⊥$ 直线l于点E，点M、N同时开始运动，各自达到相应的终点时停止运动，设运动时间为t秒．当 $△ M D C$ 与 $△ C E N$ 全等时，求t的值．

查看试题解析