黑龙江省龙东地区2023年中考数学试卷
试卷更新日期:2023-07-04 类型:中考真卷
一、选择题(每小题3分,共30分)
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
3. 一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )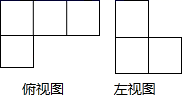 A、4 B、5 C、6 D、74. 已知一组数据的平均数是1,则这组数据的众数是( )A、-3 B、5 C、-3和5 D、1和35. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( )
A、4 B、5 C、6 D、74. 已知一组数据的平均数是1,则这组数据的众数是( )A、-3 B、5 C、-3和5 D、1和35. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( )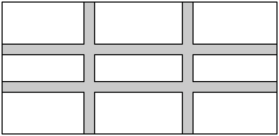 A、 B、 C、或 D、6. 已知关于x的分式方程的解是非负数,则的取值范围是( )A、 B、 C、且 D、且7. 某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )A、5种 B、6种 C、7种 D、8种8. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( )
A、 B、 C、或 D、6. 已知关于x的分式方程的解是非负数,则的取值范围是( )A、 B、 C、且 D、且7. 某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )A、5种 B、6种 C、7种 D、8种8. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( ) A、 B、 C、 D、9. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( )
A、 B、 C、 D、9. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( ) A、 B、 C、 D、10. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
A、 B、 C、 D、10. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤二、填空题(每小题3分,共30分)
-
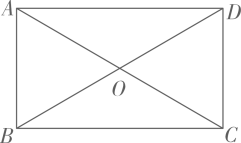
11. 据交通运输部信息显示:2023年“五一”假期第一天,全国营运性客运量约5699万人次,将5699万用科学记数法表示为 .12. 函数 中,自变量x的取值范围是 .13. 如图,在矩形中对角线 , 交于点 , 请添加一个条件 , 使矩形是正方形(填一个即可)
 14. 一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .15. 关于的不等式组有3个整数解,则实数的取值范围是 .16. 如图,是的直径,切于点A,交于点 , 连接 , 若 , 则 .
14. 一个不透明的袋子中装有3个红球和2个白球,这些小球除标号外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .15. 关于的不等式组有3个整数解,则实数的取值范围是 .16. 如图,是的直径,切于点A,交于点 , 连接 , 若 , 则 .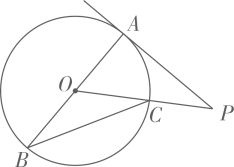 17. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .18. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
17. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .18. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
 19. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .20. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
19. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .20. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
三、解答题(满分60分)
-
21. 先化简,再求值: , 其中 .22. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , .
 (1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).23. 如图,抛物线与轴交于两点,交轴于点 .
(1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).23. 如图,抛物线与轴交于两点,交轴于点 .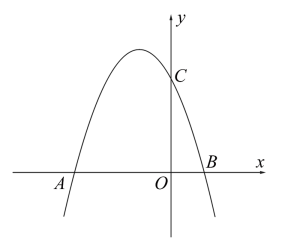 (1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.24. 某中学开展主题为“垃圾分类,绿色生活”的宣传活动、为了解学生对垃圾分类知识的掌握情况,该校团委在校园内随机抽取了部分学生进行问卷调查,将他们的得分按A:优秀,B:良好,C:合格,D:不合格四个等级进行统计,并绘制了如下不完整的条形统计图和扇形统计图.
(1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.24. 某中学开展主题为“垃圾分类,绿色生活”的宣传活动、为了解学生对垃圾分类知识的掌握情况,该校团委在校园内随机抽取了部分学生进行问卷调查,将他们的得分按A:优秀,B:良好,C:合格,D:不合格四个等级进行统计,并绘制了如下不完整的条形统计图和扇形统计图. (1)、这次学校抽查的学生人数是人;(2)、将条形图补充完整;(3)、扇形统计图中C组对应的扇形圆心角度数是;(4)、如果该校共有2200人,请估计该校不合格的人数.25. 已知甲,乙两地相距 , 一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距 , 货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离与货车行驶时间之间的函数图象,结合图象回答下列问题:
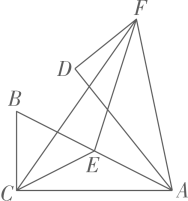
(1)、这次学校抽查的学生人数是人;(2)、将条形图补充完整;(3)、扇形统计图中C组对应的扇形圆心角度数是;(4)、如果该校共有2200人,请估计该校不合格的人数.25. 已知甲,乙两地相距 , 一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距 , 货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离与货车行驶时间之间的函数图象,结合图象回答下列问题: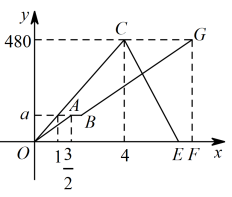 (1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .26. 如图①,和是等边三角形,连接 , 点F,G,H分别是和的中点,连接 . 易证: .
(1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .26. 如图①,和是等边三角形,连接 , 点F,G,H分别是和的中点,连接 . 易证: .若和都是等腰直角三角形,且 , 如图②:若和都是等腰三角形,且 , 如图③:其他条件不变,判断和之间的数量关系,写出你的猜想,并利用图②或图③进行证明.
 27. 2023年5月30日上午9点31分,神舟十六号载人飞船在酒泉发射中心发射升空,某中学组织毕业班的同学到当地电视台演播大厅观看现场直播,学校准备为同学们购进A,B两款文化衫,每件A款文化衫比每件B款文化衫多10元,用500元购进A款和用400元购进B款的文化衫的数量相同.(1)、求A款文化衫和B款文化衫每件各多少元?(2)、已知毕业班的同学一共有300人,学校计划用不多于14800元,不少于14750元购买文化衫,求有几种购买方案?(3)、在实际购买时,由于数量较多,商家让利销售,A款七折优惠,B款每件让利m元,采购人员发现(2)中的所有购买方案所需资金恰好相同,试求m值.28. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.
27. 2023年5月30日上午9点31分,神舟十六号载人飞船在酒泉发射中心发射升空,某中学组织毕业班的同学到当地电视台演播大厅观看现场直播,学校准备为同学们购进A,B两款文化衫,每件A款文化衫比每件B款文化衫多10元,用500元购进A款和用400元购进B款的文化衫的数量相同.(1)、求A款文化衫和B款文化衫每件各多少元?(2)、已知毕业班的同学一共有300人,学校计划用不多于14800元,不少于14750元购买文化衫,求有几种购买方案?(3)、在实际购买时,由于数量较多,商家让利销售,A款七折优惠,B款每件让利m元,采购人员发现(2)中的所有购买方案所需资金恰好相同,试求m值.28. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.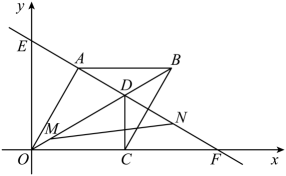 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.