陕西省西安市2022-2023学年八年级下册5月月考数学试卷
试卷更新日期：2023-07-04 类型：月考试卷
一、选择题(每小题3分，共30分)
-
1. 下列代数式中，是分式的是（ ）A、 B、 C、 D、2. 若代数式有意义，则实数x的取值范围是（ ）A、x≠-5 B、x≠0 C、x≠5 D、x>-53. 下列条件中，不能判定四边形ABCD是平行四边形的是（ ）A、 ， B、AB＝CD，AD＝BC C、OA＝OC，OB＝OD D、 ， AD＝BC4. 关于x的方程有增根，则k的值是（ ）A、0 B、3 C、2 D、-35. 如图，在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=7，EF=3，则BC长为（ ）
A、9 B、10 C、11 D、126. 一个多边形的内角和等于1440°，则它是几边形（ ）A、六 B、八 C、九 D、十7. 下列正多边形的组合中，不能镶嵌的是（ ）A、正方形和正三角形 B、正方形和正八边形 C、正三角形和正十二边形 D、正方形和正六边形8. 如图，将平行四边形ABCD沿对角线BD折叠，使点A落在E处．若∠1＝56°，∠2＝42°则∠A的度数为（ ）
A、108° B、109° C、110° D、111°9. 如图，△ABC中，AD平分∠BAC，E是BC中点，AD⊥BD，AC＝7，AB＝3，则DE的值为（ ）
A、1 B、 C、2 D、10. 如图，P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若S四边形AHPE＝3，S四边形PFCG＝5，则S△PBD为（ ）
A、0.5 B、1 C、1.5 D、2二、填空题(每小题3分，共21分)
-
11. 若式子的值为0，则x的值为 ．12. 如果一个多边形每个外角都是18°，那么这个多边形的边数是 ．13. 化简的结果为 ．14. 如图，平行四边形ABCD的对角线AC、BD交于点O，过点O作OM⊥AC，OM交AD于M，连接CM，如果△CDM的周长为8，则平行四边形ABCD的周长为 ．
15. 如图，将一条宽度为1和一条宽度为2的两条纸条叠放在一起，使得∠ABC＝60°，则四边形ABCD的面积为 ．
16. 如图，在▱ABCD中，AD＝3cm，动点P以每秒0.5cm的速度从点A向点D运动，另一动点Q以每秒1cm的速度从点C出发，在BC间往返运动，P、Q两点同时出发，当点P到达点D时停止运动(同时Q点也停止)，若P，D，Q，B四点组成的四边形是平行四边形时，则运动时间为
秒．
17. 如图，在△ABC中，∠ABC＝60°，∠BAC＝45°，AB＝6，P为AB边上一动点，以PA，PC为邻边作平行四边形PAQC，则对角线PQ的最小值为 ．
三、解答题
-
18. 解方程．(1)、(2)、19. 先化简，再求值．
， 请从-1，1，2中选择一个合适的数作为a的值代入求值．
20. 如图，在△ABC中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且CF＝3BF，连接DB，EF．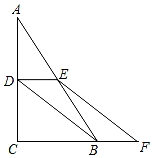
(1)、求证：四边形DEFB是平行四边形；(2)、若∠ACB＝90°，AC＝12cm，DE＝4cm，求四边形DEFB的周长．21. 某地计划修建一条长48千米的乡村公路，已知甲工程队修路的速度是乙工程队修路速度的1.5倍，乙工程队单独完成本次修路任务比甲工程队单独完成多20天．(1)、求甲、乙两个工程队每天各修路多少千米?(2)、已知甲工程队修路费用为20万元/千米，乙工程队修路费用为15万元/千米．甲工程队先单独修路若干天后，接到其它任务需要离开，剩下的工程由乙工程队单独完成．若要使修路总时间不超过55天，总费用低于820万元，且甲工程队所修路程需为整数，请问共有几种修路方案?哪种方案最省钱?22. 如图，在平行四边形ABCD中，AF平分∠BAD交BC于点F，CE平分∠BCD交AD于点E．
(1)、若AD＝10，AB＝5，求CF的长；(2)、连接BE与AF相交于点G，连接DF与CE相交于点H，连接GH，EF相交于点O，求证：GH和EF互相平分．23. 如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A，C两点的坐标分别为(4，0)，(-2，3)．将▱OABC先向右平移4个单位后，再向下平移1个单位，得到▱NPQM．
(1)、请你直接写出点N，M的坐标；(2)、▱NPQM与▱OABC的重叠部分的形状是 ， 重叠部分的面积是；(3)、点E是x轴上一动点，在直线OB上是否存在点D，使得以O，N，D，E为顶点的四边形为平行四边形?若存在，请求出满足条件的所有点D、点E的坐标；若不存在，请说明理由．