内蒙古赤峰市2023年中考数学试卷
试卷更新日期:2023-07-04 类型:中考真卷
一、选择题(每小题只有一个选项符合题意,请将该选项的序号按要求在答题卡上的指定位置涂黑.每小题3分,共42分)
-
1. 化简的结果是( )A、 B、20 C、 D、2. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.以下剪纸中,为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2023年5月19日是第13个“中国旅游日”.文化和旅游部公布的数据显示,今年“五一”假期国内游出游合计人次,同比增长 . 将数字用科学记数法表示为( )A、 B、 C、 D、4. 如图,数轴上表示实数的点可能是( )
3. 2023年5月19日是第13个“中国旅游日”.文化和旅游部公布的数据显示,今年“五一”假期国内游出游合计人次,同比增长 . 将数字用科学记数法表示为( )A、 B、 C、 D、4. 如图,数轴上表示实数的点可能是( )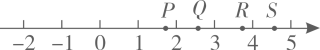 A、点P B、点Q C、点R D、点S5. 下列运算正确的是( )A、 B、 C、 D、6. 2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑,某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为A,B,C,D四个等级(A:非常了解;B:比较了解;C:了解;D:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.根据统计图信息,下列结论不正确的是( )
A、点P B、点Q C、点R D、点S5. 下列运算正确的是( )A、 B、 C、 D、6. 2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑,某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为A,B,C,D四个等级(A:非常了解;B:比较了解;C:了解;D:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.根据统计图信息,下列结论不正确的是( ) A、样本容量是 B、样本中C等级所占百分比是 C、D等级所在扇形的圆心角为 D、估计全校学生A等级大约有人7. 已知 , 则的值是( )A、6 B、 C、 D、48. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( )
A、样本容量是 B、样本中C等级所占百分比是 C、D等级所在扇形的圆心角为 D、估计全校学生A等级大约有人7. 已知 , 则的值是( )A、6 B、 C、 D、48. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( ) A、16,6 B、18,18 C、16,12 D、12,169. 化简的结果是( )A、1 B、 C、 D、10. 如图,圆内接四边形中, , 连接 , , , , . 则的度数是( )
A、16,6 B、18,18 C、16,12 D、12,169. 化简的结果是( )A、1 B、 C、 D、10. 如图,圆内接四边形中, , 连接 , , , , . 则的度数是( ) A、 B、 C、 D、11. 某校在劳动课上,设置了植树、种花、除草三个劳动项目.九年一班和九年二班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( )A、 B、 C、 D、12. 用配方法解方程时,配方后正确的是( )A、 B、 C、 D、13. 某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 , 母线长为30 , 为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
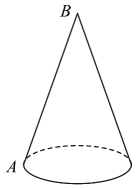
A、 B、 C、 D、11. 某校在劳动课上,设置了植树、种花、除草三个劳动项目.九年一班和九年二班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( )A、 B、 C、 D、12. 用配方法解方程时,配方后正确的是( )A、 B、 C、 D、13. 某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 , 母线长为30 , 为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )v
 A、 B、 C、 D、14. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( )
A、 B、 C、 D、14. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( ) A、①②③ B、②④ C、①③④ D、①②③④
A、①②③ B、②④ C、①③④ D、①②③④二、填空题(请把答案填写在答题卡的相应横线上.每小题3分,共12分)
-
15. 分解因式: =.16. 方程的解为 .17. 为发展城乡经济,建设美丽乡村,某乡对地和地之间的一处垃圾填埋场进行改造,把原来地去往地需要绕行到地的路线,改造成可以直线通行的公路 . 如图,经勘测,千米, , , 则改造后公路的长是千米(精确到千米;参考数据: , , , ).
 18. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .
18. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .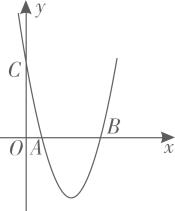
三、解答题(在答题卡上解答,答在本试卷上无效;解答时要写出必要的文字说明、证明过程或演算步骤.共8题,满分96分)
-
19.(1)、 计算:(2)、解不等式组:20. 已知:如图,点M在的边上.

求作:射线 , 使 . 且点N在的平分线上.
作法:①以点O为圆心,适当长为半径画弧,分别交射线 , 于点C,D.
②分别以点C,D为圆心.大于长为半径画弧,两弧在的内部相交于点P.
③画射线 .
④以点M为圆心,长为半径画弧,交射线于点N.
⑤画射线 .
射线即为所求.
(1)、用尺规作图,依作法补全图形(保留作图痕迹);(2)、根据以上作图过程,完成下面的证明.证明:∵平分 .
∴ ,
∵ ,
∴ , ( ).(括号内填写推理依据)
∴ .
∴ . ( ).(填写推理依据)
21. 某校甲乙两班联合举办了“经典阅读”竞赛,从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩,并对数据(成绩)进行了收集、整理,分析.下面给出了部分信息.【收集数据】
甲班10名学生竞赛成绩:85,78,86,79,72,91,79,71,70,89
乙班10名学生竞赛成绩:85,80,77,85,80,73,90,74,75,81
【整理数据】
班级
甲班
6
3
1
乙班
4
5
1
【分析数据】
班级
平均数
中位数
众数
方差
甲班
80
a
b
51.4
乙班
80
80
80,85
c
【解决问题】根据以上信息,回答下列问题:
(1)、填空: , , ;(2)、请你根据【分析数据】中的信息,判断哪个班成绩比较好,简要说明理由:(3)、甲班共有学生45人,乙班其有学生40人.按竞赛规定,80分及80分以上的学生可以获奖,估计这两个班可以获奖的总人数是多少?22. 某集团有限公司生产甲乙两种电子产品共8万件,准备销往东南亚国家和地区.已知2件甲种电子产品与3件乙种电子产品销售额相同:3件甲种电子产品比2件乙种电子产品的销售多元.(1)、求甲种电子产品与乙种电子产品销售单价各多少元?(2)、若使甲乙两种电子产品的销售总收入不低于万元,则至少销售甲种电子产品多少件?23. 定义:在平面直角坐标系中,当点N在图形M的内部,或在图形M上,且点N的横坐标和纵坐标相等时,则称点N为图形M的“梦之点”. (1)、如图①,矩形的顶点坐标分别是 , , , , 在点 , , 中,是矩形“梦之点”的是;(2)、点是反比例函数图象上的一个“梦之点”,则该函数图象上的另一个“梦之点”H的坐标是 , 直线的解析式是 . 当时,x的取值范围是 .(3)、如图②,已知点A,B是抛物线上的“梦之点”,点C是抛物线的顶点,连接 , , , 判断的形状,并说明理由.24. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , .
(1)、如图①,矩形的顶点坐标分别是 , , , , 在点 , , 中,是矩形“梦之点”的是;(2)、点是反比例函数图象上的一个“梦之点”,则该函数图象上的另一个“梦之点”H的坐标是 , 直线的解析式是 . 当时,x的取值范围是 .(3)、如图②,已知点A,B是抛物线上的“梦之点”,点C是抛物线的顶点,连接 , , , 判断的形状,并说明理由.24. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , . (1)、求证:是切线;(2)、若 , , 求的长.25. 乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
(1)、求证:是切线;(2)、若 , , 求的长.25. 乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)、在平面直角坐标系中,描出表格中各组数值所对应的点 , 并画出表示乒乓球运行轨迹形状的大致图象; (2)、①当乒乓球到达最高点时,与球台之间的距离是 , 当乒乓球落在对面球台上时,到起始点的水平距离是 ;
(2)、①当乒乓球到达最高点时,与球台之间的距离是 , 当乒乓球落在对面球台上时,到起始点的水平距离是 ;②求满足条件的抛物线解析式;
(3)、技术分析:如果只上下调整击球高度 , 乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274 , 球网高为15.25 . 现在已经计算出乒乓球恰好过网的击球离度的值约为1.27 . 请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).26. 数学兴趣小组探究了以下几何图形.如图①,把一个含有角的三角尺放在正方形中,使角的顶点始终与正方形的顶点重合,绕点旋转三角尺时,角的两边 , 始终与正方形的边 , 所在直线分别相交于点 , , 连接 , 可得 .
 (1)、【探究一】
(1)、【探究一】如图②,把绕点C逆时针旋转得到 , 同时得到点在直线上.求证:;
(2)、【探究二】在图②中,连接 , 分别交 , 于点 , . 求证:;
(3)、【探究三】把三角尺旋转到如图③所示位置,直线与三角尺角两边 , 分别交于点 , . 连接交于点 , 求的值.