黑龙江省大庆市肇源县2022-2023学年八年级下册6月月考数学试卷
试卷更新日期:2023-07-04 类型:月考试卷
一、选择题
-
1. 将一元二次方程化成一般式后,二次项系数和一次项系数分别为( )A、3,5 B、3,1 C、 , D、3,2. 下列选项中,平行四边形、矩形、菱形、正方形共同具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、每条对角线平分一组对角3. 若= , 则的值为( )A、1 B、 C、 D、4. 如图, , 若 , 则的值是( )
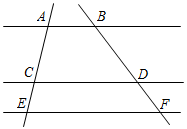 A、2 B、 C、 D、35. 一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A、2 B、 C、 D、35. 一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A、20个 B、28个 C、36个 D、32个6. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( ) A、
A、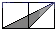 B、
B、 C、
C、 D、
D、 7. 在长度为1的线段上有一点P.满足 , 则长为( )A、 B、 C、 D、8. 用换元法解方程 , 若设 , 则原方程可化为( )A、 B、 C、 D、9. 根据下面表格中的对应值:
7. 在长度为1的线段上有一点P.满足 , 则长为( )A、 B、 C、 D、8. 用换元法解方程 , 若设 , 则原方程可化为( )A、 B、 C、 D、9. 根据下面表格中的对应值:x
3.24
3.25
3.26
ax2+bx+c
﹣0.02
0.01
0.03
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
A、x<3.24 B、3.24<x<3.25 C、3.25<x<3.26 D、x>3.2610. 如图,正方形的对角线 , 相交于点 , 点是上一点,交于点 , 连接 , 交于点 , 连接则下列结论:①;②;③若平分 , 则;④;⑤四边形的面积是正方形面积的其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤二、填空题
-
11. 方程的根为 .12. 一个六边形六边长分别为 , , , , , , 另一个与它相似的六边形的最短边为 , 则其周长为 .13. 我市某公司前年缴税40万元,今年缴税48.4万元.该公司缴税的年平均增长率为 .14. 菱形中,和是一对邻角,若 , 则度.15. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是 .16. 如图,在平行四边形中,E为的中点,交于F,若 , 则 .
 17. 已知关于x的一元二次方程(m﹣1)x2+2x+1=0有实数根,则m的取值范围是 .18. 在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,在内部作正方形,使正方形四个顶点都落在该三角形的边上或顶点上.则正方形落在x轴正半轴上的顶点坐标为 .
17. 已知关于x的一元二次方程(m﹣1)x2+2x+1=0有实数根,则m的取值范围是 .18. 在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,在内部作正方形,使正方形四个顶点都落在该三角形的边上或顶点上.则正方形落在x轴正半轴上的顶点坐标为 .三、解答题
-
19. 配方法解方程: .20. 公式法解方程: .21. 如图,菱形的对角线 , , 、交于点O,于E,求长.
 22. 将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌子上.(1)、从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)、先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.23. 如图,将矩形沿向上折叠,使点落在边上的点处.若 , , 求的长.
22. 将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌子上.(1)、从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)、先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.23. 如图,将矩形沿向上折叠,使点落在边上的点处.若 , , 求的长. 24. 已知关于x的方程有两个不相等的实数根.(1)、求m的取值范围.(2)、若两个实数根分别是 , , 且 , 求m的值.25. 某种商品进价为每件50元,若以每件60元出售,每天可售出800件.经市场调查发现,若每件商品售价每提高5元,则每天要少卖100件.求该商品应如何定价,才能使每天卖出该商品的利润为12000元?26. 在中,过点作于点 , 点在上, , 连接、 .
24. 已知关于x的方程有两个不相等的实数根.(1)、求m的取值范围.(2)、若两个实数根分别是 , , 且 , 求m的值.25. 某种商品进价为每件50元,若以每件60元出售,每天可售出800件.经市场调查发现,若每件商品售价每提高5元,则每天要少卖100件.求该商品应如何定价,才能使每天卖出该商品的利润为12000元?26. 在中,过点作于点 , 点在上, , 连接、 . (1)、求证:四边形是矩形;(2)、若平分 , , 求的长.
(1)、求证:四边形是矩形;(2)、若平分 , , 求的长.

