北京市海淀区一零一集团2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 4的算术平方根是( )A、-2 B、2 C、 D、2. 在平面直角坐标系 中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列运算正确的是( )A、 B、 C、 D、4. 已知二元一次方程x+7y=5,用含x的代数式表示y,正确的是( )A、 B、 C、 D、5. 如图,直线 , 相交于点 , 分别作 , 的平分线 , . , 则的度数是( )
 A、 B、 C、 D、6. 图,面积为7的正方形ABCD的顶点A在数轴上,且表示的数为1,若点E在数轴上(点E在点A的右侧),且AB=AE,则点E所表示的数为( )
A、 B、 C、 D、6. 图,面积为7的正方形ABCD的顶点A在数轴上,且表示的数为1,若点E在数轴上(点E在点A的右侧),且AB=AE,则点E所表示的数为( ) A、 B、 C、1+ D、+27. 如图,四边形 , 是延长线上一点,下列推理正确的是( )
A、 B、 C、1+ D、+27. 如图,四边形 , 是延长线上一点,下列推理正确的是( ) A、如果那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么8. 关于式子(为实数),下列结论中错误的是( )A、式子一定有平方根 B、当时,式子有最小值 C、无论为何值,式子的值一定是有理数 D、式子的算术平方根一定大于等于19. 已知方程组 , 则x-y的值是( )A、2 B、-2 C、0 D、-110. 在平面直角坐标系中,对于点 , 如果点的纵坐标满足 , 那么称点为点的“关联点”.如果点的关联点坐标为 , 则点的坐标为( )A、 B、 C、或 D、或
A、如果那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么8. 关于式子(为实数),下列结论中错误的是( )A、式子一定有平方根 B、当时,式子有最小值 C、无论为何值,式子的值一定是有理数 D、式子的算术平方根一定大于等于19. 已知方程组 , 则x-y的值是( )A、2 B、-2 C、0 D、-110. 在平面直角坐标系中,对于点 , 如果点的纵坐标满足 , 那么称点为点的“关联点”.如果点的关联点坐标为 , 则点的坐标为( )A、 B、 C、或 D、或二、填空题
-
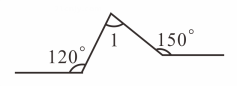
11. 在平面直角坐标系中,将点向上平移5个单位长度得到点B,则点B坐标为12. 举例说明命题“两个无理数、的和一定是无理数”是假命题, , .13. 已知点的坐标为 , 直线轴,并且 , 则点的坐标为 .14. 某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行,已知第一次转过的角度,第三次转过的角度,则第二次拐弯角(∠1)的度数是 .
 15. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为,现有一根竿和一条绳索,用绳索去量竿,绳索比竿长6尺;如果将绳索对半折后再去量竿,就比竿短6尺.设绳索长x尺,竿长y尺,可列出符合题意的方程组为 .16. 在我校初一年级举行的“古诗词大赛”中,有小晴、小贝、小敏三位同学进入最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分分别为 , , ( , 且 , , 均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.下表是三位选手在每轮比赛中的部分得分情况:
15. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为,现有一根竿和一条绳索,用绳索去量竿,绳索比竿长6尺;如果将绳索对半折后再去量竿,就比竿短6尺.设绳索长x尺,竿长y尺,可列出符合题意的方程组为 .16. 在我校初一年级举行的“古诗词大赛”中,有小晴、小贝、小敏三位同学进入最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分分别为 , , ( , 且 , , 均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.下表是三位选手在每轮比赛中的部分得分情况:第一轮
第二轮
第三轮
第四轮
第五轮
第六轮
最后得分
小晴
26
小贝
12
小敏
10
根据题中所给信息,下列说法正确的是 . (填序号)
①可求得;
②每轮比赛第二名得分为2分;
③小敏一定有两轮(且只有两轮)获得第3名;
④小贝每轮比赛都没有获得第1名.
三、解答题
-
17. 计算:18. 求出下列等式中的值.(1)、(2)、19. 解方程组:20. 完成下面的解题过程.
已知:如图, , 平分 , 求 .
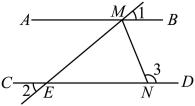
解:∵( )
又∵
∴
∴( )
∴ ▲ ( )
∵
∴
∵平分
∴
∴ ▲ .
21. 如图所示的是天安门周围的景点分布示意图,若以正东、正北方向为轴、轴的正方向建立坐标系,表示电报大楼的点的坐标为 , 表示王府井的点的坐标为 , 请解决下面的问题: (1)、在图中画出相应的平面直角坐标系,并写出美术馆的坐标;(2)、“天安门—故宫—景山”所在的直线称为北京城的中轴线,在王府井的小奇同学如果要在最短的时间内(速度相同)赶到中轴线上,则小奇应该直接到达中轴线上的点的坐标为 , 理论依据为 .22. 我们规定用表示一对数对,给出如下定义:记 , (其中 , ),将与称为数对的一对“和谐数对”.例如:的一对“和谐数对”为和 .(1)、数对的一对“和谐数对”是;(2)、若数对的一对“和谐数对”相同,则的值为;(3)、若数对的一个“和谐数对”是 , 直接写出的值 .23. 小明和小智在游戏中把五个相同的曲别针环环相扣,每个曲别针的长度为15毫米,厚度为1毫米,如果把这个曲别针环拉直(如图所示),则这个曲别针环拉直后长为多少呢?两位同学思考后分别给出了思路:
(1)、在图中画出相应的平面直角坐标系,并写出美术馆的坐标;(2)、“天安门—故宫—景山”所在的直线称为北京城的中轴线,在王府井的小奇同学如果要在最短的时间内(速度相同)赶到中轴线上,则小奇应该直接到达中轴线上的点的坐标为 , 理论依据为 .22. 我们规定用表示一对数对,给出如下定义:记 , (其中 , ),将与称为数对的一对“和谐数对”.例如:的一对“和谐数对”为和 .(1)、数对的一对“和谐数对”是;(2)、若数对的一对“和谐数对”相同,则的值为;(3)、若数对的一个“和谐数对”是 , 直接写出的值 .23. 小明和小智在游戏中把五个相同的曲别针环环相扣,每个曲别针的长度为15毫米,厚度为1毫米,如果把这个曲别针环拉直(如图所示),则这个曲别针环拉直后长为多少呢?两位同学思考后分别给出了思路:
小明:如下图,我只要分别把后面的每段长度算出来,相加就可以;

小智:我采用的是平移的思想,先假设五个曲别针不是环环相扣,而是紧密排列成下图

此时总长为毫米,每两个曲别针环环相扣,相当于把右边的曲别针向左平移了一定的长度,然后用减去所有的平移长度就可以算出来了.
请完成下面的问题:
(1)、这个曲别针环长为毫米;(2)、请根据小智的思路列出相应的算式: .24. 某校组织“衫衫来了,爱心义卖”活动,购进了黑白两种纯色的文化衫共200件,进行DIY手绘设计后出售,所获利润全部捐给“太阳村”.每种文化衫的成本和售价如下表:白色文化衫
黑色文化衫
成本(元)
6
8
售价(元)
20
25
假设文化衫全部售出,共获利3040元,求购进两种文化衫各多少件?
25.(1)、下面是小李探索的近似值的过程,请补充完整:我们知道面积是2的正方形的边长是 , 且 . 设 , 可画出如下示意图.
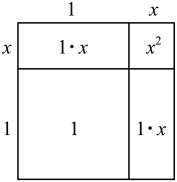
由面积公式,可得 .
略去 , 得方程 .
解得 . 即 .
(2)、容易知道 , 设 , 类比(1)的方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)26. 平面内有两个锐角与 , 点在直线的上方,保持不动,且的一边 , 另一边与直线相交于点 . (1)、若 , , 且位置如图1,当点 , , 在同一条直线上(即点与点重合)时,;(2)、若 , , , 当点 , , 不在同一条直线上,画出图形并求的度数(用含 , 的式子表示).27. 对于实数 , 表示不小于的最小整数,例如: , , . 点是轴右侧的点,已知点 , , 我们把(三角形)叫做点的取整三角形.
(1)、若 , , 且位置如图1,当点 , , 在同一条直线上(即点与点重合)时,;(2)、若 , , , 当点 , , 不在同一条直线上,画出图形并求的度数(用含 , 的式子表示).27. 对于实数 , 表示不小于的最小整数,例如: , , . 点是轴右侧的点,已知点 , , 我们把(三角形)叫做点的取整三角形. (1)、已知点 , 直接写出点的坐标;(2)、已知点 , 且点的取整三角形面积为5,直接写出的取值范围:;(3)、若点的取整三角形面积为2,请在下面的坐标系中画出所有满足条件的点的区域(用阴影表示,能取到的边界用实线表示,不能取到的边界用虚线表示).
(1)、已知点 , 直接写出点的坐标;(2)、已知点 , 且点的取整三角形面积为5,直接写出的取值范围:;(3)、若点的取整三角形面积为2,请在下面的坐标系中画出所有满足条件的点的区域(用阴影表示,能取到的边界用实线表示,不能取到的边界用虚线表示).