安徽省合肥市八校联考2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 如果 $\sqrt{x - 1}$ 在实数范围内有意义，那么x的取值范围是（）

A、 $x > 1$ B、 $x ≥ 1$ C、 $x \leq 1$ D、 $x < 1$

查看试题解析
2. 下列根式中属于最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\frac{1}{\sqrt{2}}$

查看试题解析
3. 在 $▱ A B C D$ 中，已知∠A=60° ，则∠D 的度数是（）

A、60° B、90° C、120° D、30°

查看试题解析
4. 下列四组数中不是勾股数的是（　　）

A、3，4，5 B、2，3，4 C、5，12，13 D、8，15，17

查看试题解析
5. 下列四个算式中正确的是（　　）

A、 $\sqrt{8} \div \sqrt{2}$ ＝2 B、 $\sqrt{(- 2)^{2}} = - 2$ C、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{6}$ D、 $2 \sqrt{3} \times 2 \sqrt{2} = 2 \sqrt{6}$

查看试题解析
6. 如图， $A B = A C$ ，则数轴上点C所表示的数为（）.

A、 $\sqrt{5} + 1$ B、 $\sqrt{5} - 1$ C、 $- \sqrt{5} + 1$ D、 $- \sqrt{5} - 1$

查看试题解析
7. 适合下列条件的△ABC中，直角三角形的个数为（）
①a= $\frac{1}{3}$ ，b= $\frac{1}{4}$ ，c= $\frac{1}{5}$ ②a=6，∠A=45°；③∠A=32°，∠B=58°；④a=7，b=24，c=25 ⑤a=2，b=2，c=4．

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 直角三角形斜边的平方等于两条直角边乘积的2倍，这个三角形有一个锐角是（）

A、15° B、30° C、45° D、60°

查看试题解析
9. 如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是在14，则DM等于（）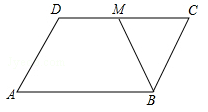

A、1 B、2 C、3 D、4

查看试题解析
10. 矩形具有而菱形不具有的性质是（）

A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等

查看试题解析
11. 如图，平行四边形ABCD的对角线相交于点O，且AD＞AB，过点O作OE⊥AC交AD于点E，连接CE，若平行四边形ABCD的周长为20，则△CDE的周长是（）

A、10 B、11 C、12 D、13

查看试题解析
12. 如图，某数学兴趣小组开展以下折纸活动：①对折矩形纸片ABCD ，使AD和BC重合，得到折痕EF ，把纸片展开；②再一次折叠纸片，使点A落在EF上，并使折痕经过点B ，得到折痕BM ，同时得到线段BN ．观察探究可以得到∠NBC的度数是（）

A、20° B、25° C、30° D、35°

查看试题解析

二、填空题

13. 比较大小：-3 $\sqrt{2}$ -2 $\sqrt{3}$

查看试题解析
14. 如果最简二次根式 $\sqrt{1 +a}$ 与 $\sqrt{4 a - 2}$ 是同类二次根式，那么a=.

查看试题解析
15. 实数 $a$ 在数轴上的位置如图所示，则 $| a - 1 | + \sqrt{{(a - 2)}^{2}} =$ ．

查看试题解析
16. 如图，长方形 $A B C D$ 中， $A B = 3 cm$ ， $A D = 9 cm$ ，将此长方形折叠，使点B与点D重合，折痕为 $E F$ ，则 $△ A B E$ 的面积是．

查看试题解析
17. 如图是一个三级台阶，它的每一级的长、宽、高分别为20dm、3 dm、2 dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是 dm．

查看试题解析
18. 观察下列各式：① $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ；② $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}} = \frac{3}{2}$ ；③ $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ， …请用含 $n (n \geq 1)$ 的式子写出你猜想的规律：.

查看试题解析

三、解答题

19. 计算：

(1)、 $(\sqrt{24} - \sqrt{2}) - (\sqrt{8} + \sqrt{6})$

(2)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div \sqrt{2}$

(3)、 $(2 \sqrt{3} + \sqrt{6}) (2 \sqrt{3} - \sqrt{6})$

(4)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{6}$

查看试题解析
20. 若实数x，y满足 $y = \sqrt{x - 1} + \sqrt{1 - x} + 2$ ，求 $\frac{\sqrt{x + 1}}{y - 1}$ 的值．

查看试题解析
21. 直线l过正方形 $A B C D$ 顶点B，点A、C到直线l距离分别是1和2，求正方形边长．

查看试题解析
22. 如图，点 $E$ 是正方形 $A B C D$ 内一点，将 $Δ A B E$ 绕点 $B$ 顺时针旋转 $9 0^{∘}$ 到 $Δ C B E^{'}$ 的位置，若 $A E = 1 ， B E = 2 ， C E = 3$ ，求 $∠ B E^{'} C$ 的度数．

查看试题解析
23. 如图， $▱ A B C D$ 中，点 $E 、 F$ 在对角线 $A C$ 上，且 $A E = C F$ ．求证：四边形 $B E D F$ 是平行四边形．

查看试题解析
24. 如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF.

(1)、求证：△AOE≌△DFE；

(2)、判定四边形AODF的形状并说明理由.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D ， E ， F$ 分别是 $A C ， A B$ 的中点，O是 $D F$ 的中点， $E O$ 的延长线交线段 $B D$ 于点G，连结 $D E ， E F ， F G$ ．

(1)、求证：四边形 $D E F G$ 是平行四边形．

(2)、当 $A D ＝ 5 ， D C = 2$ 时，求 $F G$ 的长．

查看试题解析
26. 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交CE的延长线于点F．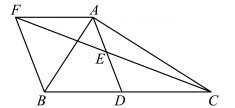

(1)、求证：四边形ADBF是菱形；

(2)、若AB＝8，菱形ADBF的面积为40，求AC的长．

查看试题解析
27. 问题情境：在数学活动课上，我们给出如下定义：顺次连按任意一个四边形各边中点所得的四边形叫中点四边形．如图（1），在四边形 $A B C D$ 中，点 $E$ ， $F$ ， $G$ ， $H$ 分别为边 $A B$ ， $B C$ ， $C D$ ， $D A$ 的中点．试说明中点四边形 $E F G H$ 是平行四边形．探究展示：勤奋小组的解题思路：


反思交流：

(1)、①上述解题思路中的“依据1”、“依据2”分别是什么？
依据 $1 ：$ 　       ；依据 $2 ：$ 　　；

②连接 $A C$ ，若 $A C = B D$ 时，则中点四边形 $E F G H$ 的形状为　                  ；并说明理由；

创新小组受到勤奋小组的启发，继续探究：

(2)、如图（2），点 $P$ 是四边形 $A B C D$ 内一点，且满足 $P A = P B$ ， $P C = P D$ ， $∠ A P B = ∠ C P D$ ，点 $E$ ， $F$ ， $G$ ， $H$ 分别为边 $A B$ ， $B C$ ， $C D$ ， $D A$ 的中点，猜想中点四边形 $E F G H$ 的形状为          ，并说明理由；

(3)、若改变（2）中的条件，使 $∠ A P B = ∠ C P D = 90 °$ ，其它条件不变，则中点四边形 $E F G H$ 的形状为　　．

查看试题解析